
 |
 |
![]()
Contents |
Committee | Preface
| Ch 1 | Ch 2 |
Intro to Ch 3-9 | Ch 3
| Ch 4 | Ch 5 |
Ch 6 | Refs for Part 1
| Other Reports | Ch 7
| Ch 8 | Ch 9
The power to reason mathematically is a natural human capacity. Young children enter school already curious about number and
size, and with ideas about how to join, remove, and split quantities. Mathematics instruction in the elementary years can---should---be
designed to cultivate this curiosity. Encouraged to solve problems, children become aware of their ideas; and as they learn to
analyze their own, their classmates, and their teachers thinking, these ideas become more refined and many-sided. It is during
these early years that young students lay down those habits of reasoning upon which later achievement in mathematics will
crucially depend.
Teaching elementary mathematics requires both considerable mathematical knowledge and a wide range of pedagogical skills. For
example, teachers must have the patience to listen for, as well as the ability to hear, the sense---the logic---in
children's mathematical ideas. They need to see the topics they teach as embedded in rich networks of interrelated concepts, know
where, within those networks, to situate the tasks they set their students and the ideas these tasks elicit. In preparing a
lesson, they must be able to appraise and select appropriate activities, and choose representations that will bring into focus the
mathematics on the agenda. Then, in the flow of the lesson, they must instantly decide which among the alternative courses of
action open to them will best sustain productive discussion.
It is by now widely acknowledged that many practicing teachers were not adequately prepared by the mathematics instruction they
received to meet these challenges. As K-12 students---often even in the primary grades---they
lost their curiosity about mathematics. When the rules and procedures one is taught are not conceptually anchored, memorization
must pass for understanding, and mathematics becomes an endless, senseless parade of disparate facts, definitions, and procedures.
College students who today choose to become teachers are by and large still products of such K-12 instruction. Even if those who opt to teach middle- or high-school-level mathematics have experienced their mathematics education positively, many who choose elementary teaching have not. Intimidated by mathematics, the latter generally avoid mathematics courses wherever possible.
It seems, then, that we are caught in a vicious cycle: poor K-12 mathematics instruction produces ill-prepared college
students, and undergraduate education often does little to correct the problem. Indeed, some universities mandate next to no
mathematics coursework for the prospective elementary teacher. However, simply increasing the number of required credit hours is
no solution---courses that allow students to get by using the same stratagems that got them through K-12 just
perpetuate the problem.
In order to break this cycle, college students with weak mathematics backgrounds must have opportunities to reconnect with their own capacities for mathematical thought. Those among them who decide to enter the classroom and are willing to engage the conceptual riches of the elementary curriculum can become effective mathematics teachers. But they, just like the children they will someday teach, must have classroom experiences in which they become reasoners, conjecturers, and problem solvers.
Future teachers will need to connect fundamental concepts to a variety of situations, models, and representations. They will have to learn to notice patterns and think about why those patterns hold; pose their own questions and know what sorts of answers make sense; look for connections among different methods for solving the same problem or different ways of representing the same quantity. In short, developing these new mathematical habits means learning how to continue learning.
This is a daunting agenda. But if teachers are to help their students become strong mathematical thinkers, it must be met. And the medium through which this agenda can be realized is the very mathematics they are charged with teaching in the realms of number and operations, geometry, early algebraic thinking, and data.
Conventional belief has it that elementary school mathematics is simple and to teach it requires only learning prescribed facts and computational algorithms. However, recent work has revealed the conceptual richness of this early content, demonstrating that teaching elementary school mathematics can be intellectually challenging. Though each of us once inhabited the mathematical world of the young child, that world is lost to most of us. To re-enter it, Deborah Ball and Hyman Bass argue in a recent paper,
one needs to be able to deconstruct one's own mathematical knowledge into less polished and final form, where elemental components are accessible and visible. We refer to this as decompression. Paradoxically, most personal knowledge of subject matter knowledge, which is desirably and usefully compressed, can be ironically inadequate for teaching. In fact, mathematics is a discipline in which compression is central. Indeed, its polished, compressed form can obscure ones ability to discern how learners are thinking at the roots of that knowledge. Because teachers must be able to work with content for students in its growing, not finished state, they must be able to do something perverse: work backward from mature and compressed understanding of the content to unpack its constituent elements. (2000a, p. 98)
Ball and Bass's description of the challenge the elementary teacher faces in connecting to the mathematical world of the child
holds for the instructor of the mathematically naļve adult. In a college course, prospective teachers' ingenuous questions will
require instructors to "decompress'' their mathematical knowledge to find responses satisfying to both mathematician
and teacher.
Although some questions elementary-school teachers pose may be stimulating, others are certain to be very disturbing. Instructors teaching teachers for the first time will occasionally feel dismay, or even shock. How can such basic notions not be understood? What is there to think about? But the gaps in these teachers' mathematical backgrounds are consequences of systemic rather than personal failings, and it is essential that, recalling this, instructors work to maintain the necessary stance of interest, generosity, and respect.
To repeat, the challenge is to work from what teachers do know---the mathematical ideas they hold, the
skills they possess, and the contexts in which these are understood---so they can move from where they are to
where they need to go. For their instructors, as we have seen, this means learning to understand how their students think. The
habits of abstraction---of compression---and deductive demonstration, characteristic of the way
mathematicians present their work, have little to do with the ways children build their mathematical world, experientially,
modeling concepts on actions---counting out, dividing up, comparing heights or ages. . . . Mathematics courses
for teachers must aim, first of all, at helping them develop ways of giving meaning to the mathematical objects under study, only
then moving on to higher orders of generality and rigor.
Chapter 3 outlines the mathematics content teachers need to know for the K-4 classroom. What follows in this chapter expands upon that discussion. Precisely because what goes on in the elementary classroom will seem alien to many readers of this document, vignettes drawn from actual lessons are used to elucidate the issues. In these scenes, children articulate their mathematical thinking, showing their teachers what they understand and where they are confused. The scenes do not exhaust the territory, but they are representative of the mathematical issues that arise in a typical classroom when mathematics teaching is organized to elicit and build upon children's thinking. (Some scenes are taken from grade 5 classrooms, but are included in the belief that what comes up in a fifth grade class is likely to come up for the fourth grade teacher, too.) The vignettes are followed by discussion of the mathematics the teachers will need in order to identify the sense in their students thinking, know when a key mathematical idea is being missed, or anticipate when significant mathematical territory is being broached. What mathematical knowledge will help teachers navigate these situations in ways that support building stronger mathematical conceptions?
These scenes taken from classrooms are not intended as models of exemplary teaching. They have been chosen, not for emulation, but to illustrate the kinds of knowledge and skills required of elementary teachers. Because lessons in which children practice routine procedures typically do not present mathematical challenges to teachers, they are not included in this document. Their absence is not meant to imply that such activities have no place in the elementary mathematics classroom.
For readers who have little contact with aspiring or practicing elementary-level teachers, excerpts from teachers learning journals and episodes from teacher education courses are also included. These are intended to communicate what teachers themselves report as new mathematical insights.
All of the vignettes are drawn from actual classrooms. Many of the scenes of elementary-level lessons are paraphrases of cases written by the teachers themselves. Others are taken from videotape or records of classroom observations. Scenes from courses for teachers and excerpts from teachers journals are based on published literature, unpublished field notes, and personal communications.
The recommendations for course content draw on research about teacher and student knowledge. They also follow from the assumption that most teachers (though certainly there are exceptions) have had few, if any, opportunities to learn content that is just now entering the elementary curriculum, particularly topics in early algebra, geometry, and statistics.
This chapter discusses teaching and learning at both elementary-school and teacher-preparation levels. To minimize confusion, the term "children'' is used to refer to elementary school students, and "teachers'' refers to both practicing and aspiring teachers.
Understanding number and operations and developing proficiency in computation have been and continue to be the core concerns of the elementary mathematics curriculum. Although almost all teachers remember traditional computation algorithms, their mathematical knowledge in this domain generally does not extend much further. Indeed, many equate the arithmetic operations with the algorithms and their associated notation. They have little inkling of how much more there is to know. In fact, in order to interpret and assess the reasoning of children learning to perform arithmetic operations, teachers must be able to call upon a richly integrated understanding of operations, place value, and computation in the domains of whole numbers, integers, and rationals.
Understanding models and interpretations of operations with whole numbers (i.e., the set of non-negative integers):
| |||||||||||||||
Developing a strong sense of place value in the base-10 number system:
| |||||||||||||||
Understanding multidigit calculations, including standard algorithms, "mental math,'' and non-standard methods commonly
created by students:
| |||||||||||||||
Developing the concepts of integer and rational number and extending the operations to these larger domains:
|
In order to begin to explore the mathematics content knowledge required for teaching at the elementary level, consider the classroom scene below, which captures children at work on subtraction.
Scene 1, from a second grade classroom: The children have been finding the difference between Jorge's height, 62'', and the height of Cinthia's little brother, Paulo, 37''. (Currently they are using inches so that the heights will be two-digit numbers. Later they will use centimeters to get three-digit numbers.) Many of the children use dots and ten-sticks to represent two-digit numbers.
| Gabriella: | (She has drawn three dots, then two ten-sticks, then two dots, and written 25.) I said, "How much does Paulo have to grow?'' so 37 plus 3 more (pointing to three dots) is 38, 39, 40, and 50 (pointing to a ten-stick), 60 (pointing to another ten-stick), 61, 62 (pointing to two dots). So this is 23 (gesturing to the three dots and two ten-sticks), 24, 25 more he has to grow to catch up with Jorge. |
| Roberto: | I shrunk the big guy down by taking away the little guy from him (gesturing to his drawing of the little guy beside the big guy and the line he drew across from the top of the little guy to the big guy). So 62 minus 37 is 25. I took three tens from the six tens and seven from the ten. That leaves three and these two are five and two tens left is 25. |
| Josué: | I did it like Gabriella but I wrote three and then my ten-sticks and two and then added them to get 25 more the little guy needs. |
| Ms. Lo Cicero: | Can someone else say in their words how Josué did it? |
| Nanci: | He used numbers and sticks to go 37 plus 3 is 40 plus 2 tens is 60 plus 2 to get to Jorge. So 2 tens and 5 is 25. |
| Ruffina: | I just counted in my mind 37, 47, 57, that's 20, then 58, 59, 60, 61, 62, so that's 5. 25. |
| Marķa: | I subtracted Paulo from Jorge like Roberto did, but I used numbers. I took one of the tens to get enough to take away the seven so that was three and two more was five ones, and there were two tens left so 25. |
| Ms. Lo Cicero: | Can someone else tell how Roberto's and Marķa's methods are alike? |
| Carlos: | They both took away the little guy to get the difference. They took away 37 from 62. |
| Ms. Lo Cicero: | Anything else? |
| Jazmin: | They both had to open a ten because there weren't seven ones to take away. So Roberto took his seven from that ten-stick. (Teacher points to show the ten-stick Roberto separated into seven and three, and looks questioningly at Jazmin.) Yes, there he took seven and left three. And Marķa took a ten from the six tens and wrote it with the ones and then took the seven to leave three. |
| Ms. Lo Cicero: | So they were both thinking about taking ones from a ten but they wrote it in different ways? |
| Several students: | Yes. |
| Letticia: | And we know other ways to write subtraction, too. |
| Ms. Lo Cicero: | Yes, you have lots of ways you show taking away and comparing, too. Whose heights should we compare next? |
(based on Hiebert et al., 1997, pp. 153-155)
Formed by an education equating mathematical strength with computational proficiency, too many teachers have been left with an
impoverished understanding of the number system. To orchestrate a classroom discussion like the one above, or those presented
below, teachers must be able to do more than demonstrate remembered procedures---for example, they must be able
to select problems that anticipate the issues their students will next need to confront, and then assess whether what the children
make of those problems advances the mathematical agenda. Such skills require much deeper understanding of number and operations
than most teachers now hold. The bulleted items discussed below identify key points of entry into the mathematics of the
elementary grades.
![]() Each operation can model a variety of actions
or situations.
Each operation can model a variety of actions
or situations.
For years, elementary textbooks have suggested that teachers teach their students to solve word problems by finding "key words'': "altogether'' means add, "left'' means subtract, etc. Beyond such superficial clues, many teachers associate each operation with just one possible action: joining with addition; taking away with subtraction; repeated addition with multiplication; and either finding the number of groups of a given size or, given the number of groups, finding the size of each group (usually not both) with division (Graeber & Tanenhaus, 1993). Hampered by their own limited understanding of the operations, teachers have had little more to offer their students. What is required is a sense of the different kinds of situations that can be modeled by each of the four basic operations.
In the classroom scene above, the teacher has selected a problem involving comparison of heights. By thinking through the situation, the children develop different solution strategies: Gabriella considers how much Paulo has to grow; Roberto thinks about "shrinking the big guy down.''
A teacher who is aware of the range of situations that can be modeled by subtraction can consciously choose problems that promote a variety of ways of thinking about the operation. The following is an example of a common "take-away'' problem: Sue Ellen had 62 cents and then bought an item for 37 cents. How much money did she then have? A second type of subtraction problem involves joining, with the starting quantity unknown: Manny went to the beach yesterday and picked up 37 shells for his shell collection. He now has 62 shells. How many shells did he have before his last visit to the beach?
Teachers must come to recognize the variety of situations---of joining, separating, and comparing, with an
unknown in various positions---that can be represented by addition and subtraction. Similarly, multiplication and
division can be associated with a rich store of interpretations: multiple groups, splitting, shrinking and stretching, counting
rectangular arrays, counting combinations. In many interpretations of multiplication (and in contrast to addition and
subtraction), the numbers are associated with different units: e.g., 3![]() 4 might model 3 bags,
each with 4 donuts. Such multiplication problems have two types of division problem as analogs: partitioning into groups of
a given size and partitioning into a given number of groups.
4 might model 3 bags,
each with 4 donuts. Such multiplication problems have two types of division problem as analogs: partitioning into groups of
a given size and partitioning into a given number of groups.
In developing more broadly based conceptions of the kinds of situations modeled by the operations, it is also important to become familiar with such other modes of representation as the number line or arrangements of blocks. Area representations of multiplication are particularly useful.
Keeping in mind Scene 1, consider a second, in which, at the start of a new unit on division, the teacher has given the class a set of what she considers division problems.
Scene 2, from a combined third/fourth grade classroom:
Jesse has 24 shirts. If he puts eight of them in each drawer, how many drawers does he use?
Vanessa writes: 24--8 = 16, 16--8 = 8, 8--8 = 0, and then writes 3 for the answer.
If Jeremy needs to buy 36 cans of seltzer water for his family and they come in packs of six, how many packs should he buy?
This time Vanessa writes: 6 + 6 = 12, 12 + 12 = 24, 24 + 6 = 30, 30 + 6 = 36. (She doesn't identify her answer.)
You go into a pet store that sells mice. There are 48 mouse legs. How many mice are there?
Matthew organizes his work in a chart of two columns:
1 m 4 l 2 m 8 l . . .
Then in a neat box he writes,
12 m
4 l = 48 l
Above the box, he writes the number 12.
The teacher wonders, what does this say about kids' understanding of division if they use all the operations except division? (based on Schifter et al., 1999a, pp. 55-57)
Scenes 1 and 2 illustrate another issue, the interrelationships of the operations, that many teachers need to work on.
![]() A given situation can be modeled by different
operations.
A given situation can be modeled by different
operations.
The "key words'' mindset leads many teachers to believe that, for any given word problem, there is just one operation that can be used to solve it correctly. However, as Scene 2 shows, a "division problem'' can be solved by adding, subtracting, or multiplying. And in Scene 1, where some children readily see their way to the solution as a process of finding a missing addend, others subtract. Instead of ruling out any of these methods as incorrect or problematic, a teacher who understands the ways operations are interrelated can seize the opportunity to explore such connections more deeply.
The children whose classroom gave rise to Scene 2 did eventually learn their division facts. With a richer understanding of
what division means and how it is related to the other operations, they were able to see how particular facts can be derived from
other facts, making the process of recall easier. (Later in the lesson from which Scene 2 derives, Matthew is given another
"division problem.'' He responds, "It's 63![]() 9. What number times 9 is 63?
Seven. . . . [I]t is [division], but my thinking is multiplication.'')
9. What number times 9 is 63?
Seven. . . . [I]t is [division], but my thinking is multiplication.'')
Understanding how the operations are related and how these relationships can be called upon in solving problems is critical for teachers if they are to interpret and advance their students thinking. Just such a revelation is recorded in this excerpt from the journal of one participant in an inservice course.
In my group we did it [159
13] the "regular way'' [using the division algorithm], then by equally distributing base-ten rods, [and then] by going around and counting out by ones. Then [the instructor] came to our group and 159
13 suddenly became 159
--13 = 146, 146--13 = 133, 133--13 = 120, . . . and so on. I had never before thought of division as directly related to subtraction. . . . As simple as it sounds that one interaction really made an impact on me, asand
were just something I did by a rote method, with not much thought as to how
,
,
, and
are all related. (Schifter et al., 1999b, p. 177)
This teacher was now resolved to bring these ideas to her fourth grade students.
Returning to Scene 1, consider that the children's methods rely on decomposing numbers into tens and ones. This highlights another set of ideas teachers must understand.
![]() The principles of place value involve
significant conceptual issues for young children and for teachers.
The principles of place value involve
significant conceptual issues for young children and for teachers.
Most teachers are readily able to identify the ones place, the tens place, etc., and can represent multidigit numbers in expanded notation. Nonetheless, they often lack understanding of core ideas: how place value permits efficient representation of numbers; that the value of each place is ten times larger than the value of the next place to the right; how a number can be decomposed into tens and ones in a variety of ways (53 can be viewed as 5 tens and 3 ones, or 4 tens and 13 ones, etc.); how the operations of addition, multiplication, and exponentiation are used in representing numbers as "polynomials in 10''; and how decimal notation allows one to determine quickly which of two numbers is larger. Teachers should be familiar with the notion of "order of magnitude'' and should have a sense of the relative magnitudes of numbers.
Not only must teachers be able to state these ideas, they must be able to recognize and apply them flexibly. One activity that has been used successfully to help teachers develop such facility asks them to create a number system using the symbols A, B, C, D, and 0 (Schifter & Fosnot, 1993). The letters allow the possibility of assigning different values to the symbols. Working in small groups and offered a set of base-five blocks as a thinking tool, teachers are asked to show how to represent large numbers in their system and to calculate with multidigit numbers. If they should get that far, they are also asked to explore divisibility and give an account of numbers smaller than 1.
Among the strategies teachers tend to pursue, the following are the most common:
| assigning the values 1, 5, 25, 125 to A, B, C, D; one counts A, AA, AAA, AAAA, B, BA, BAA, . . . | |
| assigning the values 1, 2, 3, 4, 5 to A, B, C, D, 0; one counts, A, B, C, D, 0, 0A, 0B, 0C, . . . (some teachers,
uncomfortable assigning 5 to the symbol "0,'' make up a different fifth symbol). | |
| assigning the values 1, 2, 3, 4, 0 to A, B, C, D, 0; one counts, A, B, C, D, A0, AA, AB, . . . |
The first two strategies result in number systems resembling those of the ancient Egyptians and the ancient Greeks, respectively; the third results in a place-value system.
Although it is intended that everyone eventually explore a base-five place-value system, getting there as quickly as possible is not the point of the exercise. More important is that the teachers suggest a system, explore it, encounter its limitations, and redesign it accordingly. Through this process, they discover the various properties of different number systems and gain deeper understanding of our own.
Many teachers exposed to this activity come to appreciate the kind of flexible, connected knowledge that allows them to recognize a familiar mathematical idea in a very unfamiliar setting. As one teacher wrote:
I've taught place value over and over and over again and I've told the kids, "We only have ten numerals and the way the number system works is, the place tells you the value of the number.'' I've said it a hundred times and here I went to design a system and I couldn't use the methods that I tell people over and over again. So I do feel like it was a major thing that I learned. It was worth the frustration to get what I think of as a lasting understanding of place value . . . (Schifter & Fosnot, 1993, p. 60)
![]() Multidigit calculation provides opportunities
to both deepen understanding of place value and build meanings for operations.
Multidigit calculation provides opportunities
to both deepen understanding of place value and build meanings for operations.
The following errors are commonly seen in elementary classrooms:
| 26 + 58 714 |
43 26 |
54 162 108 270 |
In these examples, children are applying their single-digit math facts but are mis-remembering their computational procedures. Because they are not thinking about the size of the numbers they start with or about what the operations do, they form no reasonable estimate of the outcome. If neither the children, nor their teachers, have learned to approach such problems with the expectation that they should make sense, it is difficult to correct the misconceptions underlying these errors.
Teachers with richly developed meanings for the operations (a sense of the variety of situations and representations associated with the operations) and a flexible understanding of place value (for example, knowing how to decompose numbers into convenient parts and operate on them) are positioned to help such children. They can recognize the strong thinking of children like Gabriella, Roberto, and their classmates in Scene 1, and they can help children who make such errors as those shown above go back to what they do understand about numbers and operations in order to help them recognize their errors.
Solving multidigit problems in their heads---"mental arithmetic''---and then sharing the
strategies they employ, is an especially useful exercise. Teacher educators have found (Schifter et al., 1999b) that many students
come to courses believing that conventional algorithms offer the only valid methods of computation. Those who invent their own
strategies often feel sheepish, as if they are relying on "crutches,'' or are embarrassed by their lack of
"sophistication.'' Once the hold of these prejudices is loosened and they begin to maneuver about the number system more
fluently, they begin to see how the base-ten structure can be used flexibly and efficiently.
As various methods of calculation are encountered, teachers must consider the logic behind each: Does this method always work? Some need to consider why very basic procedures are justified, say, 58 + 24: 50 + 20 = 70, 8 + 4 = 12, 70 + 12 = 82. In one seminar, a teacher watching a video of second graders solving problems such as this, blurted out, "I can imitate this method to apply to other numbers, but I don't see why it works. It's just another meaningless algorithm to me!'' In this situation, representations such as blocks or number lines, which help teachers think about what the operations do, can help them see a justification for the procedures. Some teachers must think through the general principle that addends can be decomposed and the parts recombine in any order, yet conserve the sum; or that when subtracting, if the same amount is added to or subtracted from both quantities, the difference remains constant.
Other, more complicated procedures are often challenging to teachers. Consider the following steps, commonly devised by primary
grade children, for solving 35 -- 16:
| 30 |
| 5 |
| 20 |
This procedure raises such questions for teachers as: Why is the 1 subtracted rather than added? Will this work for any subtraction problem, even one with numbers larger than two digits? When does this method apply and what comparable method can be used when it doesn't? Can the steps of this procedure be articulated as an algorithm? A college student writing in her journal, excerpted below, touches on these issues.
I have been amazed at how this "thing'' we call place value has come to make real sense to me. This goes beyond the traditional breakdown of a number. For example, I know the number 84 is comprised of 8 tens and 4 ones, but the way I look at doing a math problem is beginning to change. For example, when I look at the problem 84 + 76, I can now do it several different ways. I can look at 84 + 76 and say to myself:80 + 70 = 150 and 6 + 4 = 10; add 150 + 10 = 160; or
84 + 70 = 154 and 154 + 6 = 160; or I can revert to my traditional method:
84
+ 76
160
Furthermore, I am able to apply this same type of thinking to subtraction problems. I have more difficulties with subtraction problems, but I am working on increasing my comfort level. What I discovered to be very interesting were the many ways a subtraction problem could be broken down. . . . The example of 35--16 was a great one. This led to many different discussions. I was able to look at this problem and say:
5
--6 =--1; 30--10 = 20; and 20--1 = 19.However, a fellow student made it even clearer by lining up the problem in a more systematic way:
3 | 5
--1 | 6
20 |--1
=
19
(Student journal, spring, 1999)
This aspiring teacher, her classmates, and others enrolled in comparable classes certainly know the computation algorithms
before beginning the course. What they learn is flexibility in decomposing numbers, figuring out how to recombine them to perform
the operations, and thinking about the operations in terms of the actions they model. The numbers they are operating on remain in
view and do not get lost in a thicket of disconnected digits. (Thus, "3 -- 1''; in the computation above is
correctly recognized as a representation of 30 -- 10, which equals 20.)
Similarly, with multidigit multiplication and division, learners (both children and teachers) first think in terms of groups in order to sort out calculation procedures. Again, teachers can begin an exploration of multiplication through practicing mental calculations. Then they can analyze their own, their classmates', and children's methods of calculation. Once the idea of rectangular array is introduced into thinking about groups, the area model, in particular, brings to light the partial products of two-digit multiplication. Later, these ideas can be formalized as the distributive property.
![]() Comparing procedures can make the reasoning
behind algorithms transparent
Comparing procedures can make the reasoning
behind algorithms transparent
In Scene 1, Ms. Lo Cicero asks the class how Roberto's and Marķa's methods are alike. In this way, she highlights particular steps in the procedures and draws students' attention to analogous lines of reasoning in the different representations. For another example of comparing procedures, consider the following scene.
Scene 3, from a fifth grade classroom: The class has been given the homework problem 72834. One child, Henry, presents this solution method:
| 680 + 34 714 |
|
728 14 |
Henry explains to the class, "Twenty 34s plus one more is 21. I knew I was pretty close. I didn't think I could add any more 34s, so I subtracted 714 from 728 and got 14. Then I had 21 remainder 14.''
Another child, Michaela, presents her solution:
21
34 | 728
68
48
34
14
Michaela describes the steps of the conventional division algorithm: "34 goes into 72 two times and that's 68. You gotta minus that, bring down the 8, then 34 goes into 48 one time.''
Apparently, their teacher has not shown the conventional division algorithm to her students, and Michaela's classmates say they don't understand her solution. Asked to explain, Michaela takes the class through the steps again, but with the same response. Then the teacher asks the class to compare the two procedures to identify similar parts, assisting them by inserting a "0'' next to Michaela's "68'' so that the children could more easily see where Henry's 680 shows up in Michaela's process. Through the discussion that ensues, using Henry's solution as a point of reference, some of Michaela's classmates can begin to see the justification for the steps she had taken.
(based on NCTM, 2000, pp. 153-154)
The reasoning behind Henry's method is clear to him and his classmates. But when Michaela presents the conventional long division algorithm with its more efficient notation, the rationale for her procedure eludes both her and her classmates. The teacher recognizes the parallel reasoning behind the two methods and draws her students' attention to it, thus giving them access to what was an initially opaque process.
The steps of the conventional algorithms, particularly for multidigit multiplication and division, are often every bit as mystifying to teachers as they are to children. The former, too, can compare procedures, devised by themselves or by students, or by other cultures, to bring to light their conceptual bases.
It is also useful to examine commonly applied incorrect procedures for solving multidigit multiplication problems, such as those instantiated in the following strategies observed in the work of teachers and children.
|
Teachers or children calculated 16 |
Writing: |
|
|
|
|
|
|
Operating on the tens, operating on the ones, and adding the results. |
(10 |
|
|
|
|
|
|
Subtracting 2 from one factor and adding it to the other; then operating. |
14
|
|
|
|
|
|
|
Rounding up to the nearest tens, operating, and subtracting off what had been added on. |
(20
|
Each of these incorrect methods derives from misapplying additive procedures. After all, when adding 16 + 28, one can operate on the tens, operate on the ones, and add the results, etc. By analyzing these procedures, teachers have opportunities to deepen their understanding of multiplication and the distributive property, and to become sensitive to the tendency to extend additive procedures to multiplicative situations.
Presenting and exploring these various methods of calculation highlights for teachers the differences among the operations. In addition and subtraction, the units are the same; in multiplication and division, more than one unit is involved. In addition or subtraction, one can decompose the addends or both the minuend and subtrahend, respectively. In multiplication, additively decomposing both factors frequently makes the calculation more complex. And in division, additively decomposing the divisor is not useful. Up to now, this discussion has been confined to the arithmetic of whole numbers. And children do begin to learn about numbers through counting. Soon, though, the world of number expands to include integers and rationals. In order to support children through this transition, teachers, too, must have explored these new concepts.
![]() As with whole numbers, teachers
must learn to give meaning to operations with integers.
As with whole numbers, teachers
must learn to give meaning to operations with integers.
Many young children are exposed to numbers less than 0 outside of school, through discussions of weather in the
wintertime, say, or by keeping track of scores in some of their games. In an example cited above, a second grader says that
5 - 6 equals "one in the hole" and knows how to use that idea to compute 35 --
16. However, in general, operating with integers presents new issues.
Scene 4, from a third grade classroom: The children have been working with an image of an elevator to represent integers. The ground floor is 0; floors are numbered up to 12 to the roof and to
--12 below the ground level. The children write number sentences to model "elevator trips." For example, if a person starts on the third floor and goes down seven floors, the trip is represented as 3--7 =--4 . The children can do this task well and come up with significant observations:
Nathan:
Any number below zero plus that same number above zero equals zero.
Ofala:
Any number take away double that number would equal that same number only below zero.
However, the teacher is concerned about the limitations of the elevator representation. For example, it allows the children to think about subtracting a positive integer as "going down" or about subtraction as the distance between floors, but the representation does not help the children develop a sense of "taking away" numbers less than zero. Nor could they make sense of certain addition expressions, e.g. 6 + (
--6) .
(based on Ball, 1993)
Knowing the rules for computing with integers is insufficient for understanding operations with numbers less than zero. As with whole-number operations, teachers and children must learn to think of the variety of situations that can be modeled by the operations. Now, however, as the numbers represent both magnitude and direction, the situations increase in complexity.
![]() Fractions introduce a new kind of
number.
Fractions introduce a new kind of
number.
Children are introduced to rational numbers through their work with fractions. Although most young children are familiar with the numbers 1/2, 1/4, and perhaps 3/4, the idea of fraction is challenging. To many, these numbers represent a quantity less than one, or, perhaps, part of a whole, but they might also talk about how "your half is bigger than my half" or be unable to interpret the meaning of, say, 2/3. And even when children seem to understand the meaning of fraction in some situations, that understanding often proves fragile and context dependent. For example, in a class of third graders who had been working on fractions for some weeks, the question arose, Which is larger, 4/4 or 5/5? Some argued for 4/4 because the parts are larger; others, for 5/5, because there are more parts. No one argued they were equal (Ball & Wilson, 1996).
Adults are generally unable to recall a time when their concept of number was exhaustively defined by the
experience of counting whole numbers. Yet, listening to children being introduced to the idea of fraction and realizing how this
challenges their very notion of number, offers adults an opportunity to think through how the concept of number expands as one
moves from the system of integers to rationals. It is no longer merely a matter of counting units. Instead, one must now count the
number of units in one quantity, count the number of units in a second quantity, and derive a third number---a
new kind of number---that places the first quantity in relation to the second (Behr & Hiebert,
1988; Carpenter, Fennema, & Romberg, 1993).
Many children, and older students as well, see fractions only as pairs of natural numbers plugged into arithmetic procedures. So, for example, in the second National Assessment of Educational Progress, when students were asked to pick an estimate for 12/13 + 7/8 from the choices, 1, 2, 19, and 21, most chose the latter two, presumably having combined either their numerators or their denominators. They failed to recognize that 12/13 and 7/8 are each quantities close to 1 and, thus, their sum is close to 2 (Carpenter et al., 1981).
For teachers to be able to perceive the mathematical ideas children must put together in order to develop the idea of fraction, their own understanding of the concept must be expanded. The same number created by finding the part of a whole can also be seen as an expression of division (further discussed below), as a point on the number line, as a rate, or as an operator.
Most teachers know what a fraction is under at least one of its interpretations, but they often lack a sense of
relative size. Having memorized a method for finding a common denominator and comparing numerators, they cannot determine, say,
which of a pair is larger---
5/7 or 7/9? or 5/8 or
7/12?---without applying that procedure. Working with area diagrams, teachers
can explore such fraction pairs and learn to use other strategies, e.g., given common numerators, comparing the denominators; or
considering how much smaller each fraction is than 1, or how much larger than
1/2. Such observations can, in turn, be applied to more cumbersome pairs of fractions.
![]() Developing meaning for
calculating with fractions enriches understanding of both fractions and operations.
Developing meaning for
calculating with fractions enriches understanding of both fractions and operations.
The following vignette illustrates two major mathematical ideas---unit and fraction as quotient---that
need to be investigated by teachers and children, too.
Scene 5, from a fifth grade classroom: To work on a representation of "3 divided by 15," children produce the scenario "three pizzas need to be shared among 15 people," and solve the problem by dividing each of the pizzas into five slices. When the teacher changes the problem to 3 divided by 16, there is not such a neat solution.
One child suggests cutting each circle into 16 pieces. Another, whose scenario is "share 3 pieces of cheese among 16 mice," says that if you divide each piece into five slices, one mouse won't get any. Another girl says she should have divided each of the three pieces of cheese into six slices. A debate ensues about what to do with the extra slices. Some of the students think it would work to divide each of the leftover slices into eight pieces, and they are challenged to explain to their classmates how they have figured out that it will be eight. Another issue for debate is what each of the little pieces should be called: one sixteenth? one eighth? one forty-eighth? (Each of the slices, it has been agreed, is one sixth of a piece of cheese.)

(based on Lampert and Ball, 1998, pp. 139-141)
The first major mathematical idea, "unit," is central to work with fractions. In Scene 5, the children
correctly suggest that the small bits of cheese could be represented as
1/16, 1/8, or 1/48
---depending on the unit chosen. The second major idea is the relationship between fraction and division. Many
teachers have considered fractions only as parts of a single-unit whole---e.g., 3/16
involves dividing a single whole into 16 equal pieces and taking three of those. The idea that 3/16 might mean three wholes divided equally into 16 portions is new to
them. And they would have difficulty explaining how the quantity 3/16 is the same as the quantity 1/6 + 1/48.
(Lampert & Ball, 1998, p. 142)
In the Mathematics and Teaching through Hypermedia Project, prospective teachers work on these ideas, analyzing videotape of the fifth graders' discussion summarized in Scene 5, and supplemented by problems the teachers solve for themselves. For example, they are given the following assignment:
|
Think about the following interpretations of 3 divided by 17.
| |
|
Write or draw an explanation of how you might do each of these "fair share" problems. | |
|
Now try dividing the same quantities of pizza, money, and donuts among 15 people. What different math gets called
into play? | |
|
Now try dividing the same quantities of pizza, money, and donuts between 2 people. What different math gets called
into play this time? (p. 143) |
This assignment requires teachers to work with different kinds of units, prompting them to investigate different representations and the computations associated with them. Changing the number of people involved in the problem challenges the teachers to consider what it is about the numbers that makes the problem come out as it does; teachers then make conjectures about what would happen with other numbers. The issue of unit arises again when adding fractions. Consider the problem, One batch of muffins needed 3/4 cup of flour. The second batch needed 2/4 cup of flour. How much flour was used in both batches? In one class of fourth graders working on this problem, some children argued for the answer 5/4, others 5/8. All were looking at the following representation (Heaton, 2000).

In order to help her students work out why the correct answer is 5/4, first the teacher needed to see why 5/8 made sense to some of her students, what would be a question in this context whose answer is 5/8 (e.g., If you start with 2 cups of flour, how much of the flour do you need for the two batches?). Understanding how 5/8 could make sense to some of her students, she was in a better position to help them see why 5/4 is the sum of 3/4 + 2/4.
Addition and subtraction require working with single units, but multiplication and division involve more than one.
This is precisely what is so difficult about devising word problems or diagrams for, say,
3/4![]() 1/2: What is
the unit for
3/4? for
1/2? for the quotient? And how does that shift when multiplying
3/4
1/2: What is
the unit for
3/4? for
1/2? for the quotient? And how does that shift when multiplying
3/4![]() 1/2? On the other
hand, sorting out these issues can bring to light the reasoning, so elusive to both children and adults, behind the
invert-and-multiply algorithm. (These ideas are further elaborated in the chapter on mathematics for middle grades teachers.)
1/2? On the other
hand, sorting out these issues can bring to light the reasoning, so elusive to both children and adults, behind the
invert-and-multiply algorithm. (These ideas are further elaborated in the chapter on mathematics for middle grades teachers.)
![]() Decimal fractions extend the
ideas of place value to numbers less than 1; as with calculations with common fractions, decimal computation can enrich
understanding of the operations.
Decimal fractions extend the
ideas of place value to numbers less than 1; as with calculations with common fractions, decimal computation can enrich
understanding of the operations.
Scene 6, from a fifth grade classroom: In September, the teacher had given the class a set of word problems, among them, "Rob wants to read one hundred pages of his book before his next conference in seven days. How many pages should he read each day?" Now, two months later, she asks her students to look at the problem again, but to find the answer on a calculator. The children all report, 14.285714. After reviewing an earlier discussion about the interpretation of their original answer, 14 remainder 2, the teacher asks "What is the `.285714' in the calculator's answer?"
The class begins to talk about this and, after a few minutes, Jeremy raises his hand. "I think I get it. In the 14.285714 it's like the 2 is a paragraph and the 8 is a sentence and the 5 is a word and the 7 is a letter and the 1 is part of a letter. I don't know what the 4 is. Only the 14 [the two left-most digits] really counts anyway. The other pieces are really small, especially after you get beyond the sentences." "That's pretty interesting," the teacher says. But recognizing the limitations of Jeremy's metaphor, she offers him an opportunity to qualify it: "Does it make sense to you that it could work that way?"
"Well, it doesn't really make sense," he answers. "I mean, you don't have pieces of words to be read and things like that. It does make sense in some ways though; like how I said, it's really only the first few numbers that make a difference. The rest are too small to matter." (based on Schifter et al., 1999c, pp. 108-110)
Many children and teachers, too, believe decimals bring with them a new set of rules to remember, but the main principles that underlie decimal fractions are the same as those that govern whole numbers. Precisely because they are tacit with respect to whole numbers, formerly unproblematic concepts now need to be considered, thus providing an opportunity to return to whole numbers with new insights.
For example, in Scene 6, a fifth grade class is presented with an eight-digit number between 14 and 15 and the children are challenged to interpret the digits to the right of the decimal point. Although Jeremy's metaphor is limited (a paragraph is not necessarily 2/10 of a page; a sentence is rarely 8/10 of a paragraph), it does bring him and his classmates to an important observation: "It's really only the first few numbers that make a difference. The rest are too small to matter." Indeed, this can be said of any multidigit number, whole ones included. The digits to the left are more significant than those to the right in determining the magnitude of the number. (This is the basic idea behind scientific notation; and the same principle is highlighted in stem-and-leaf representations of data.)
Like the fifth graders in Scene 6, teachers, too, need to develop meanings for the digits to the right of the
decimal point. Having them create their own representations of decimals (with blocks or diagrams) provides opportunities to bring
out misunderstandings and highlight issues that need to be explicit for teachers---what is the value of each
place and how do the digits combine to represent a single quantity?
Teachers must come to see that any number can be approximated arbitrarily closely by finite decimals. The study of repeating decimals invites work with the calculator and, especially given the calculator's finite capacity, exploration of its limitations. Why is it that a calculator cannot exactly represent 1/3? How can you characterize all fractions that have finite representations?
To summarize this discussion of decimals, consider the following journal excerpt, by an inservice instructor who asked her class to compare whole number and decimal addition.
People at first posited many differences, but by the end of the discussion came to see none! For example, the first thing stated as a difference was that you line whole numbers up from right to left and then you line decimals up from the decimal point. Then someone suggested that if you have two decimals with the same number of places, you also line them up from the right and that, in fact, you are always (no matter what kind of numbers you are dealing with) lining up like places with like places and that this was a similarity, not a difference. . . .
Another difference mentioned was that when you add decimals, the quantities got smaller, but when you add whole numbers, the quantities got bigger. People actually thought about this for a moment. I suggested we add some decimals, so they proposed .15 + .16. Everyone then stated that no, in fact, even decimal addition makes numbers bigger [when only positive addends are under consideration]. Someone stated authoritatively that when you multiply, the result ends up being smaller. I asked disingenuously how this could be since just last session people were telling me that multiplication was nothing more nor less than repeated addition. If addition of decimals produces larger quantities, how could multiplication of decimals produce smaller quantities? Some people laughed. . . .
The third difference was proposed by Nancy, who said that the places got smaller as you go to the right of the decimal and larger as you go to the left. I asked her to come up and show us what she meant and she approached the board, pulled up sharply, and said, "Oops, never mind!" as she figured out that even to the right of the decimal, the farther to the left you go, the bigger the number.
Then someone suggested that regrouping changes as you move across the decimal. I wondered how, and several people said it worked the same way regrouping works in whole number addition, but that the places had different names.
(Yaffee, personal communication, 1997)
This recap of a discussion among teachers working to understand number and operations highlights several themes. First is the habit of noticing superficial characteristics of calculation procedures. When dealing with rule making at this level, one must remember different rules for the different kinds of numbers. Moreover, when relying solely on memory, one is likely to come up with such misremembered "facts" as "adding decimals produces a sum smaller than the addends," but with no resources to challenge them. Returning to basic principles, however, different rules may merge into one. The arithmetic for decimals is essentially the same as for whole numbers.
Second, shallow or mistaken ideas, such as those offered in this recap, can sit alongside correct understandings. When the classroom environment is safe enough to bring such notions out into the open, they can be challenged, corrected, replaced, or modified.
And third, this journal entry illustrates how the basic themes of place value and operations recur in the context of work with rational numbers.
One might have noticed that, in this discussion of number and operations, the formal statements of properties
(some prefer to call them "the laws of algebra") have not played a central role. To many teachers at the elementary
level, algebraic notation obscures rather than illuminates. Introducing formal axioms in the expectation that teachers will be
struck by the beauty and logical economy of our number system is naļve. Only after they have done the kind of work described
above---have come to know the various kinds of situations modeled by the operations, developed a variety of
representations for them, and worked with these representations to explore calculation with whole numbers, integers, and rationals---can
they make sense of algebraic notation. Without it, mechanical application of rules (commutativity, associativity, etc.) is likely
to leave them with those familiar feelings of disconnection.
Work with algebra is discussed in the following section.
Although the study of algebra and functions generally begins at the upper-middle- or high-school grades, some core concepts and practices are accessible at a much earlier age. If teachers are to cultivate the development of these ideas in the elementary grades, they must understand those concepts and practices and recognize how they are manifested in the mathematical thinking of young children.
|
Generalizing arithmetic and quantitative reasoning:
| |||||||||
|
Discovering how the field axioms govern arithmetic:
| |||||||||
|
Understanding functions:
|
When children begin their study of algebra in middle or high school, they learn a new language, an efficient way
of representing properties of operations and relationships among them. Now they are expected to make meaning for such sentences
as,
| If a > b and c > d, then a + c > b + d. | ||
| a2b2 | = | (ab)2 |
| (x + 1)2 | = |
x2 + 2x + 1 |
| (2n + 1) + (2m + 1) | = | 2(n + m + 1) |
If, in earlier grades, students lose their ability to make sense of mathematics and, as a consequence, can attach no meaning to arithmetic expressions, they have nothing on which to build their algebra. On the other hand, to those already familiar with those properties and relationships, the challenge is learning the conventional system of notation.
When the elementary classroom is designed to encourage and build upon children's thinking---where
students pursue their own questions---we find them interested in formulating and testing generalizations (Ball
& Bass, 2000a, 2000b; Carpenter & Levi, 1999; Russell et al., 1999). This is particularly evident in their work on
calculation and number theory topics: evens and odds, square numbers, factors. Children's interest in articulating these
generalizations provides an opportunity for them to explore the ideas they will later learn to express in algebraic form. At the
same time, it provides an opening to work on methods of justification.
Many elementary teachers have shared the situation of the child who enters algebra class without a sound background in arithmetic. They, too, struggled through their courses, memorizing rules for manipulating symbols. If, on the other hand, prospective teachers are offered a course that helps them make sense of number and operations (as described above), then they are prepared to learn to use algebraic notation to express relationships that have meaning for them.
However, to be able to support children in the classroom, teachers will need more than fluency in algebra. They must appreciate the power of generalization, be able to recognize when children are approaching this territory, and understand what counts as a justification.
![]() To build on children's capacities
to articulate their observations and to generalize requires teachers who understand the importance of generalization and who
command a variety of methods of justification and forms of representation.
To build on children's capacities
to articulate their observations and to generalize requires teachers who understand the importance of generalization and who
command a variety of methods of justification and forms of representation.
Scene 7, from a kindergarten classroom: The children are in pairs playing a version of the card game, War. For each round, they each put down two cards and whoever has the larger sum takes the four cards. Myra and Janie have just laid out their cards and Myra declares, "I get these." Janie protests, "But you didn't count yet! I might have more." Myra explains, "My two numbers are more than your two numbers, so when you put them together, mine is more."
(based on Seyferth, field notes, 1995)
Scene 8, from a second grade classroom: The children have become intrigued by square numbers (squares of natural numbers) and have set out to learn whatever they can from them. They work in small groups and, as each group makes a new observation, a child goes to the chart paper the teacher has set up in the front of the room and writes it down. At the end of the session, the list includes the following items:
|
1, 4, and 9 are square numbers. | |
|
16, 25, 36, 49, 64, 81, and 100 are square numbers. | |
|
If you times a square number by a square number, you get a square number. | |
|
Take any square number and add two zeros to it and you will get another square number, like 4, 400. |
(based on Rigolleti, unpublished paper, 1991)
Scene 9, from a combined third/fourth grade classroom: The class was given a problem involving eight odd numbers that summed to 71. Now, in whole group, the children discuss how they know this is an impossible situation. The following arguments are offered:
|
You have to try it a bunch of times. | |
|
It goes odd, even, odd, even, odd, even [each time you add an odd number]. | |
|
I know that an odd and an odd always equal an even. [In the problem,] there are eight different kinds, so each one has a partner to equal an even and the evens can't equal up to 71. |
(based on Bastable & Schifter, in press)
In Scene 7, Myra's strategy for determining which child has the larger sum subverts her teacher's goal for the lesson. Rather than practice counting or adding, Myra reasons about quantities in general (Thompson, 1993). A teacher who recognizes the power of her observations will sacrifice her immediate objectives in order to encourage such thinking.
Given a situation similar to that depicted in Scene 8, a teacher who registers the difference between the first
and second pairs of statements can ask about the latter, will it always work? Indeed, the teacher who recognizes that the fourth
statement is a corollary of the third (understanding that the children's meaning for "add two zeros to it" is
"insert two zeros after the last digit") is positioned to assess whether any members of the class can take on that idea.
And the third and fourth graders in Scene 9 make inferences based on three different kinds of arguments: testing a conjecture on a
set of specific numbers, reasoning by extending a pattern, and forming a deductive argument. Only teachers who themselves
appreciate the differences among these different forms of justification can, in turn, help their students understand them.
Greater attention to algebraic thinking at the elementary level has encouraged teachers and researchers to look
into young children's abilities to reason with variables (Ball, 1989; Carraher et al., 2000). For example, in one first and second
grade combination class (Carpenter & Levi, 1999), students worked with such equations as,
| x + x + x |
= | 10 |
| x + y |
= | x |
| x + x | = | y |
Children working on the first equation concluded that the sentence is true when x = 5. They generated the second when asked to find "an open number sentence that is true for every number, no matter what you put in." For the third, they found a number of solutions and recognized that y must be twice as large as x. As this kind of material moves into elementary classrooms, teachers must be aware of different uses of variables: to express unknowns that can be solved, to express identities, and to express relationships between sets of numbers (Usiskin, 1988).
To work on these issues, teachers, too, must be given contexts---perhaps, like their students, to
explore factors, divisibility, square numbers---in which they can come up with their own observations and assess
the validity of their own and their classmates' claims. For elementary teachers, it is especially important that they learn to
develop arguments using, in addition to algebraic notation, representations familiar to them. For example, the third and fourth
claims in Scene 8 can be supported using an area model of multiplication. By identifying the same lines of reasoning in strategies
employing different forms of notation, teachers can now learn to give meaning to once meaningless symbols. And as they become used
to algebraic notation, they can learn to appreciate its power and flexibility, especially in comparison to geometric
representation.
For elementary teachers, an understanding of commutativity, associativity, distributivity, identities, and
inverses cannot be taken for granted. Lacking proper grounding, many will have the sense that these rules have simply been
"pulled out of the air." Rather, they should be given tasks that help them make these generalizations from their
experiences. For example, one might ask teachers to consider these properties for all four operations, devising representations or
situations to demonstrate why they work when they apply, why they don't if they don't, and then to identify any patterns they
discover. Although it may be obvious to teachers that addition and multiplication are commutative, it is not obvious that
reversing the quantities when subtracting or dividing yields the inverse. Although associativity of addition may be clear,
teachers need to think through why, for example, (10 -- 7) -- 2 results in a
smaller number than 10 -- (7 -- 2).
In one inservice class, teachers exploring these properties reported the following conclusion: "When you
reverse the numbers for subtraction, you get the opposite---except when the numbers are the same." To
understand what the teachers were saying, the instructor worked with them to represent their observation in conventional algebraic
notation: If a -- b = c, then
b -- a = -- c, except when a = b. Perplexed by this exception,
the instructor challenged them. After a few minutes of confused discussion, the teachers explained that if a = b,
then the answer is 0 both ways, not -- 0, which they called "the opposite of 0." When
asked for the opposite of 0, there was a long pause, until someone ventured, "Infinity---the opposite of
nothing is everything." This opening provided an opportunity to think about additive and multiplicative inverses, additive
and multiplicative identities, and how definition plays a role in creating a consistent system (Schifter, field notes, 1989).
With a deeper understanding of commutativity, associativity, distributivity, identities, and inverses, teachers
can return to calculation algorithms---those conventionally taught in the United States, those taught in other
countries, as well as those children frequently devise---to analyze them as applications of these properties.
![]() Solving multistep problems in a
variety of ways also provides opportunities for teachers to create meaning for algebraic notation.
Solving multistep problems in a
variety of ways also provides opportunities for teachers to create meaning for algebraic notation.
Problems conventionally solved using algebra are, in fact, accessible to elementary grade children, as well as to teachers whose algebraic skills are under-developed. For example, consider the following problem (written quite a few years ago, when we paid less for our fruit): Ten apples and 5 bananas cost $1.65, and one apple and one banana together cost $.20. What is the cost of one apple? one banana? In one course for teachers, some teams got started by pulling out colored cubes: 10 red for apples, 5 yellow for bananas. Each cube stood for the cost of a single piece of fruit and, together, the 15 cubes represented $1.65. Pairing red and yellow cubes, then discarding them, the teachers subtracted $.20 for each pair. Left with 5 red cubes worth $.65, they concluded that each was worth $.13. Therefore, a banana cost $.07.
Having solved the problem in a way that called upon their own mathematical ideas, the teachers could then
represent it algebraically. Identifying a as the cost of an apple and b as the cost of a banana, they could now see
parallels between the steps they took with the blocks and the steps of the algebraic procedure.
|
|
10a + 5b = 1.65
|
As teachers come to see how algebraic representations correspond to representations of actions modeled by other solution methods, they become more confident and skillful with algebra. From here, they can appreciate the use of algebra in problems for which other representations are too cumbersome.
![]() Work with patterns has been a
part of the K-4 curriculum, but the concept of function is new.
Work with patterns has been a
part of the K-4 curriculum, but the concept of function is new.
Scene 10, from a kindergarten classroom: The class has been working on patterns. As the teacher presents today's pattern (green, orange, brown, green, . . . ), she also writes down the number associated with each element: "1" is written under the green square, "2" under the orange, "3" under brown, "4" under green. As has been routine, the children call out what comes next: orange, brown, green. Now the teacher points to the numbers she has written to show how she has identified the place of each square and poses a new question to the class: "What color square will go in the tenth place?" Different children call out different colors, as if this were a guessing game. But Roberto speaks forcefully. He stands up, stamps his foot, and declares, "It's green! I know it's green!"
(based on Cohen, personal communication, 1994)
Scene 11, from a third grade classroom: The teacher is working with a small group of children who are interested in the surface area of towers they make out of cubes. Starting with a 1
1
2 tower, it takes some time for the children to sort out what surface area is, but eventually they conclude that 10 faces of the unit cubes show on the surface. They backtrack to look at a 1
1
1 tower before they move on to a 1
1
3 . The teacher suggests that they organize their findings into a chart.
Number of Cubes
Surface Area
1 6
2
10
3
14
She now asks the children to think about the surface area of the next larger tower. in
|
Moira: |
How many do you add? You add 4 to each one. So the next one would be 18. |
|
Teacher: |
Why are you adding 4? Do you agree that every time you add on a cube, you add on 4 to the surface area? Can you explain why? Does that make sense? |
Jeff holds a stack of five cubes. He then shows the group how he counts all the square units on each face of the tower
---5 + 5 + 5 + 5 + 2. He points to the 5 square units on each of the four vertical faces, then adds the 2 for the ends. But then he shows that it is also 4 + 4 + 4 + 4 + 4 + 2 if he counts around all the vertical square units of each cube in the tower and then adds the ends. He says it's (45) + 2 and (5
4) + 2. The others agree.
Two days later, the teacher gives the group cubes of different sizes
---with edges of 1, 2, 3, and 4---and asks what they think the surface area of each is. The children record their findings: 6, 24, 54, 96---and Jeff declares the next one is 150, though he hasn't made one that size.
The teacher asks if the group could make any rules to describe how the areas change. First Jeff says the areas were all 3
-numbers (multiples of 3). Ron says they are also counted by 6-numbers. Then he says the areas were always six times one face of the whole cube. Ron suggests that they added three 6s every time. He points out the distance between 6 and 24 is 18 and guesses the same is true for 24 to 54. When he sees the distance is 30, Jeff points out that's five 6s. They figure out it's seven 6s between 54 and 96 and observe: 3, 5, 7. So Jeff says it must be nine 6s to 150. (based on Schifter et al., in press)
Elementary teachers often create rich classroom experiences around patterns, usually beginning with a sequence of
elements (sometimes in the form of sounds or movements), where a set of elements forms a unit that is repeated. Children learn to
extend the pattern by determining and repeating the unit. Later, children have experiences with number patterns---finding
the next number, then explaining how they did it. However, teachers rarely have a sense of how this is related to the mathematics
their students will encounter in later years: specifically, that a function can be created by labeling the elements or units of a
pattern by the natural numbers. For example, the kindergartners in Scene 10 have been presented with a function, and based on the
regularity of the pattern, Roberto is able to identify the value in the range associated with a particular value in the domain.
Some of the patterns children find particularly intriguing point toward ideas that will prove significant in higher grades. For example, second graders working on square numbers notice that as they increase, a pattern forms. The numbers go up by 1, 3, 5, 7 . . . Third graders in Scene 11 notice a similar pattern for the surface area of cubes: As the length of each side increases by 1, the surface area increases by 3 sixes, 5 sixes, 7 sixes.
Those same third graders also notice a different pattern when they count the square faces on the surface of the 1
![]() 1
1
![]() n towers they build: The numbers
go up by 4. Teachers who are familiar with the characteristics of particular classes of functions
n towers they build: The numbers
go up by 4. Teachers who are familiar with the characteristics of particular classes of functions---in this case,
linear and quadratic---would have a context for their students' observations.
The children's observation that "you add 4 to each one'' is consistent with a recursive representation of
functions: f (n +1) = f (n) + 4. Jeff points out how you can look at a 5-cube tower and see the
surface area as
4 ![]() 5 + 2, approaching a representation in closed form: f (n)
= 4n + 2
. Teachers must be familiar with both.
5 + 2, approaching a representation in closed form: f (n)
= 4n + 2
. Teachers must be familiar with both.
Some of the new curricular materials for the elementary grades have children working with stories, graphs, and tables to describe situations that change over time, e.g., height, speed, distance, population. These include graphs not defined by elementary functions. The very ideas on which the children are working are content for teachers: What is the meaning of a horizontal straight line? a line tilted up? a line tilted down? What is the relationship between rate of change and accumulated change?
Those familiar with the usual college-level algebra course will recognize that it does not address the issues described in this section.
For many years, the geometry curriculum for the elementary grades mandated recognition of basic
two-dimensional shapes, measurement of length with standard and non-standard units, and the ability to apply area and perimeter
formulas for rectangles (and possibly a few other shapes). Because so many students entered high-school geometry courses
unprepared for it (Usiskin, 1987; van Hiele, 1986), topics in geometry have recently been given a more prominent role in the early
grades. Their own experience with high-school geometry notwithstanding, for most elementary teachers, much of this material---some
of it highlighted below---is new.
|
Developing visualization skills:
| |||||||||||
|
Developing familiarity with basic shapes and their properties:
| |||||||||||
|
Understanding the process of measurement:
|
|
Understanding length, area, and volume:
|
Spatial visualization---building and manipulating mental representations of two- and
three-dimensional objects and perceiving objects from different perspectives---is a critical aspect of geometric
reasoning (Battista, 1999; National Council of Teachers of Mathematics, 2000), but is a capacity few teachers have had
opportunities to develop. Helping teachers cultivate spatial sense must be an initial, and is certainly an indispensable, goal in
a geometry course.
![]() Developing spatial sense and
identifying significant features of shape are the core tasks of elementary-level geometry and the basis of what teachers have yet
to learn.
Developing spatial sense and
identifying significant features of shape are the core tasks of elementary-level geometry and the basis of what teachers have yet
to learn.
The activities illustrated in the following scenes drawn from fourth grade classrooms prove equally stimulating and challenging for teachers.
Scene 12, from a fourth grade classroom: A three-dimensional image is shown on a screen for three seconds, and the children are asked to build a copy of it with interlocking cubes. They go through this process with a set of structures, and for each one, stop to discuss how they saw the structure (Battista & Clements, 1998). The image below takes the most time to discuss because some students feel strongly that this image can only have nine cubes, but others think it could have ten.
Natalie explains that she saw three first, with two added to the top end, two more going down, and two behind these. She explains she could start with the first three and continue from that point just adding two at a time.
Sandy agrees that Natalie's shape could be correct, but says she put one on the back bottom of the first three. She feels that one could be there and no one would see it. Robby is very interested in Sandy's idea and, using her cube building, tries putting it at the same angle as on the transparency. He wants to determine whether, looking at it from this angle, the back cube could be seen. (based on Schifter et al., in press-a)
Scene 13, from a fourth grade classroom: The class has been given a set of non-regular polygons with the following directions: "If this were a cake you had to share evenly between two people, how could you cut it? You need to be able to explain how you know that each person would get the same amount of cake." Kumiko and Sarah have both divided the hexagon shown below by separating the triangle from the square.
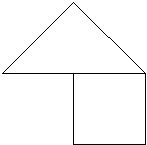
The two children have different ways to explain how they know the triangle and square are equal in area.
Kumiko:
I put the square on top of the triangle. Then I cut off the extra pieces [marked a] and put them in here [marked b].
Sarah:
I cut this part off [the triangle marked a] and moved it up to the top [the triangular space marked b].
Another child, working on the decagon below, divides it as shown.
He explains that he can take the part on the right, flip it, rotate it, and slide it, and it will fit exactly on top of the other.
(based on Tierney et al., 1998)
As do their students, so do teachers need experiences with activities, like those described in Scenes 12 and 13, that cultivate spatial sense. In Scene 12, learners construct a mental image of a three-dimensional object by analyzing it into parts, remembering the size, shape, and orientation of each, and then recombining them in correct relationship to one another. In Scene 13, learners decompose non-regular polygonal shapes into more familiar ones in order to demonstrate equal areas.
Additional activities should include exercises involving projections, cross-sections, and decompositions of common
plane figures---regular polygons and (as shown here) non-regular polygons---and solids---prisms,
cylinders, cones, pyramids, spheres. (Electronic tools that support exploration, such as dynamic geometry software, can enhance
this work.)
Another set of activities for both children and teachers involves representing three-dimensional objects in two
dimensions using a variety of methods and, given a two-dimensional representation of a three-dimensional structure, reconstructing
the original. Each method of representing three dimensions on paper preserves some features of the original object and distorts
others. Creating such representations requires that one identify and isolate those features. Learning to read them means being
able to construct mental images of a three-dimensional object from a specific set of cues. The children in Scene 12 are able to
read the figure shown and recognize that it is an ambiguous representation of a three-dimensional object---that
two possible structures fit the constraints of the problem.
Through this work, teachers can become familiar with basic two- and three-dimensional shapes: identify them, be able to draw them, know their definitions and how the shapes satisfy those definitions, recognize these shapes as parts of more complex configurations, and know some facts about them. And through this work, they can also develop different images of how shapes are composed. For example, a cube can be seen as a stack of congruent squares or as an object whose surface unfolds into a net of six squares. A tetrahedron can be seen as a stack of triangles decreasing in size or as an object whose surface unfolds into a net of four triangles.
Teachers should be able to recognize the symmetries of different polygons and solids and be familiar with some
plane isometries---reflections (flips), rotations (turns), and translations (slides). As illustrated in Scene 13,
children and teachers should be able to demonstrate congruence by using these isometries.
Although most teachers are able to identify right, acute, and obtuse angles, there is often serious confusion about exactly what angles are and what their measures mean. In mathematics courses for teachers, one hears such questions as: "How is it that both a large protractor and a small protractor agree on the measure of a given angle?'' or "How can it be that a hexagon has 720 degrees when it fits inside a circle and a circle has only 360 degrees?'' Questions like these provide an opening to discuss just what an angle is and how it is measured.
Teachers should understand the idea of angle, both as the figure formed by two rays and as angular motion. They
should understand that angles can be added, that the measure of the sum of angles is the sum of the angle measures (modulo 2![]() or 360 degrees), and that the measure of angles of a triangle sum to
180 degrees, a straight angle. And they ought to be able to devise a proof for the sum of the angle measures of a polygon.
or 360 degrees), and that the measure of angles of a triangle sum to
180 degrees, a straight angle. And they ought to be able to devise a proof for the sum of the angle measures of a polygon.
The following is frequently observed in professional development settings: Teachers asked to measure the interior
angles of a variety of polygons soon recognize a pattern---that the sum of the measures increases by 180 degrees
each time you increase the number of sides of the polygon by 1---which they can write as a formula,
(n -- 2) ![]() 180 . But then one will hear
that, "When you go from a quadrilateral to a pentagon, you add two lines, but you also take away a line. Since a line is 180
degrees, you add two but take one away, so you add 180 degrees.'' The argument is based on the idea that "a line has 180
degrees,'' but takes no notice of the angles, themselves.
180 . But then one will hear
that, "When you go from a quadrilateral to a pentagon, you add two lines, but you also take away a line. Since a line is 180
degrees, you add two but take one away, so you add 180 degrees.'' The argument is based on the idea that "a line has 180
degrees,'' but takes no notice of the angles, themselves.
Similarly, teachers who present the following diagram may claim that "Any polygon with n sides can be
divided into n -- 2 triangles. A triangle has 180 degrees. So the polygon has (n -- 2)![]() 180 degrees."
180 degrees."
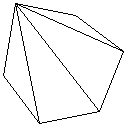
This argument sounds like the most familiar proof of this finding, but it may be that the teachers are actually paying attention to regions and not to angles. Thus, those who make this argument are often stymied when presented with this figure:

By a similar argument, the same polygon now has an angle sum of
n![]() 180. Confronted with this contradiction, teachers must now attend to which
angles of the triangles contribute to the angle sum of the polygon and express this in their arguments. The second figure
illustrates another formula
n
180. Confronted with this contradiction, teachers must now attend to which
angles of the triangles contribute to the angle sum of the polygon and express this in their arguments. The second figure
illustrates another formula
n![]() 180
180 - 360 which teachers should recognize as a
variation of the original.
The study of geometric shapes encourages the development of technical vocabulary, establishing the power of precise mathematical terminology in the communication of ideas.
![]() Everyday language and
mathematical vocabulary are used to communicate geometric ideas.
Everyday language and
mathematical vocabulary are used to communicate geometric ideas.
In newer curricular materials, children are encouraged to describe and compare shapes using vocabulary familiar to them. They talk about objects being "pointy," "tipped," or "going the wrong way." A particular rhombus might be described as a "squished square," and a cone called a "megaphone." They use words such as "corner" or "diamond," and the term "point" usually means vertex to them. Gradually, and as class discussions highlight particular features of shape, technical vocabulary is introduced.
Teachers exploring shape should also learn appropriate mathematical terms, e.g., "vertex," "side," "face," "edge," "surface area." Their work with vocabulary clarifies the purpose of precise mathematical terminology. For example, when children use the word "corner" applied to a rectangle or rectangular solid, they might be referring to any of several features. Using the words "vertex," "edge," or "angle" can eliminate ambiguity.
The word "same" is often heard in elementary mathematics discussions, but can have many meanings: Two rectangles might be said to be the same precisely because they are both rectangles, or because they are the same height, or because they are the same shape (even if of different size), or because one can exactly cover the other. On the other hand, "similar" is a common English word that has been given a precise mathematical meaning. (After a particular lesson on similarity, one teacher wrote, "I was surprised that `similar' actually has a specific definition, that `same' is less specific." Another confessed, "I thought I knew the definition, but when you [the instructor] put up rectangles that are similar, that blew my mind" [Bastable et al., in press].)
The role of mathematical definition takes on particular significance when children confront the contrast between definitions of triangle, rectangle, and square and their intuitions about which shapes are included in those categories. For example, a scalene obtuse triangle oriented so that no side is horizontal suddenly becomes a triangle, while a triangle-like object with rounded corners is now excluded.
In the following scene, a primary-grade teacher works with her students on squares and rectangles.
Scene 14, from a combined first/second grade classroom: The teacher is leading a whole-group discussion about the children's definitions of rectangle. As the children talk, the teacher writes down their key points:
|
4 sides | |
|
4 angles | |
|
4 corners |
When the teacher asks, "So what's a square?" Roberto responds, "Four sides, four corners, four angles, and it's a square." The teacher writes:
|
4 sides | |
|
4 angles | |
|
4 corners |
|
Clarisa: |
Actually, you don't need to say four corners and four angles; they're the same thing. |
|
Teacher: |
Look at what we said about squares and what we said about rectangles. |
|
Josh: |
Hey, they're the exact same thing! I'm thinking of shapes with the same definition but they're not a square or a rectangle. |
He goes to the board to show what he's thinking of:
(based on Bastable et al., in press)
Here, the teacher helps her first and second graders see that the definition of rectangle is not simply a list of salient features, but must distinguish rectangles from all other shapes.
![]() The process of measurement
involves conceptual issues, not only procedures.
The process of measurement
involves conceptual issues, not only procedures.
Although most teachers understand the use of the ruler, few are aware of the conceptual issues involved in
measurement. For example, they may not have considered explicitly the ambiguity of such words as "big" or
"size," or that objects have several measurable attributes, e.g., that a box might be measured by its height, girth,
surface area, volume, weight . . . Objects can be compared with respect to an attribute, either qualitatively (longer vs. shorter,
heavier vs. lighter) or by assigning a numerical value, i.e., its measure. To measure an attribute, one must select an appropriate
unit---for example, length must be measured by linear units, area by units that fill the plane, etc.---compare
the unit to the object, and report the number of units. Also, perhaps implicitly understood, though often a surprise when
explicitly remarked upon, smaller units yield larger counts.
Teachers should understand that measurements in the real world are approximations and how the unit chosen affects the precision of a measurement. They should be able to convert from one unit to another and use conversions to estimate measures. (For example, if the length of one's stride is approximately 2 1/2 feet and one paces a room to estimate its measure, one needs to multiply the number of paces by 2 1/2 in order to find the approximate measurement of the room in feet.) And they should know English and metric units of measure.
With regard to length, area, and volume, teachers must know what is meant by one, two, and three dimensions. A common misunderstanding is that perimeter is two dimensional since, it is argued, the perimeter of a rectangle has both length and width. Also, when asked to build a rectangular solid whose edges are double those of another, many teachers will double the length and the width, but not notice that a third dimension must also be doubled.
The following scene raises some conceptual issues involved in measuring area.
Scene 15, from a combined third/fourth grade classroom: The teacher has asked her class to consider a triangle drawn inside a 3
4 rectangle with the following constraints: one side of the triangle is a side of the rectangle of length 4; the opposite vertex of the triangle is in the middle of the opposite side of the rectangle. What is the area of the triangle? The children copy the figure onto graph paper and, because of inaccuracies in their drawings, obtain different answers. Some children count up whole and partial units to 5; others, to 6. Emil, who believes the answer is 5, considers another way to view the problem.
|
Emil: |
If you add the squares outside the triangle and add it to the triangle, you should get 12. So, since 5 + 7 = 12, you then want to get 7 on the outside. |
Omar picks up on the idea of looking outside the triangle and argues it should be 6.
|
Omar: |
The rectangle is worth 12. If you took the part that's not in the triangle and folded it up, it would make another equal triangle. The part in the middle is the same as the outside, so each part is 6. |
 |
|
| (based on Schifter et al., in press) | |
In Scene 15, third and fourth graders use what they know about partitioning shapes to figure out the area of a
particular triangle. Future lessons will include experiences first with triangles inscribed in a
3 ![]() 4 rectangle, then triangles inscribed in rectangles, encouraging the children
to apply their own reasoning as they raise the level of generality. Rather than applying area formulas by rote, these children
build a foundation for understanding why the formulas work.
4 rectangle, then triangles inscribed in rectangles, encouraging the children
to apply their own reasoning as they raise the level of generality. Rather than applying area formulas by rote, these children
build a foundation for understanding why the formulas work.
However, both children and teacher in this classroom had already done much work on area prior to this lesson. Their ideas about area did not start here. In fact, understanding the area of a rectangle cannot be taken for granted among either children or adults.
Even to children who grasp the idea of using a plane-filling unit (e.g., a square) to measure area, the structure of a rectangular array is not obvious. They must coordinate unit squares, rows composed of unit squares, columns composed of those same unit squares, and a whole, the rectangle, which can be viewed as composed of squares, of rows, or of columns.
Although teachers may not face this conceptual challenge, there is still much for them to learn. They may remember
the formula
A = L![]() W, but have no sense of how the linear units of the rectangle are
related to the units that measure area or why multiplying the linear dimensions yields the count of those units (Simon & Blume,
1994). Similar issues apply to the volume of a rectangular solid (Heaton, 1992).
W, but have no sense of how the linear units of the rectangle are
related to the units that measure area or why multiplying the linear dimensions yields the count of those units (Simon & Blume,
1994). Similar issues apply to the volume of a rectangular solid (Heaton, 1992).
Once teachers have developed facility with composing and decomposing shapes, and possess an understanding of square units and rectangular arrays, they can analyze the behavior of measures under uniform dilations, first with respect to rectangles and rectangular solids, then generalizing to other shapes.
As Scene 15 suggests, an understanding of units of area, measuring rectangles, and composition and decomposition of shape prepare one to work through the logic of the area formulas for triangles, parallelograms, and trapezoids. An understanding of units of volume and the array structure of rectangular solids allows one to extend these ideas to the volume of other prisms and cylinders. Teachers should also know the formulas for the area and circumference of a circle, for the volume of cones and pyramids, and be familiar with some demonstrations of why they work.
Another subtopic worth considering is the complex relationships among different aspects of size. For many people, the impulse is to say that if A is bigger than B with regard to one attribute, the rest of A's attributes are bigger, too (Ball, 1991; Ma, 1999). However, one can have three rectangles, A, B, and C, where A is tallest, B has the largest area, and C, the largest perimeter; or three rectangular solids D, E, and F, where D is tallest, E has the largest surface area, and F, the most volume. Exploring the different aspects of size can be expanded into a major area of study (Fitzgerald & Shroyer, 1986), by posing such questions as: Which rectangles (with sides of whole-number lengths) can be made with a perimeter of 12 cm? of 20 cm? What is the area of each? Which shape maximizes area? Which rectangles can be made with an area of 24 square cm? etc.
Statistics is the science of data, and the daily display of data by the media notwithstanding, most elementary teachers have little or no experience in this vitally important field. The statistics they need to know is naturally organized around the following three-step paradigm:
Data production: designing studies to collect data relevant to questions of interest.
Data analysis: using graphical representations, tables, and numerical summaries to find and describe patterns in the data.
Interpretation: relating the results of data analysis back to original questions and stating conclusions; if necessary, designing and implementing a further study.
Probability serves as the theoretical basis for statistical inference, a subject beyond the scope of elementary school mathematics. But probability extends beyond its role in statistics and it is important to introduce teachers to the basic concepts enumerated below.
|
Designing data investigations:
| |||||||||||
|
Describing data:
| |||||||||||
|
Drawing conclusions:
| |||||||||||
|
Developing notions of probability:
|
![]() Data studies can be designed to
address particular kinds of questions.
Data studies can be designed to
address particular kinds of questions.
Teachers begin by considering the question, What can be discovered through collecting, representing, and analyzing data?
Data can be obtained for the elementary classroom through a variety of means. Data sets are available in the principal's office, from the town clerk, or through the Internet, for example. Data are collected in science experiments, lessons in measurement, daily lunch counts or other surveys.
Yet any data collection procedure can present difficulties that must be addressed. What does one do with an incomplete data set? How does one account for inaccuracies in measurement? How can survey questions be framed to reduce ambiguity and produce analyzable data? What does one do with ambiguous data or data that do not fit predetermined categories? This very issue arises for the children in Scene 16.
Scene 16, from a third grade classroom: In a unit called Project Huff and Puff, the children measured how far they could blow various objects and collected their results. One chart showed how far each child blew a styrofoam cylinder, but when the class looked it over, they saw Robbie listed twice. He had, indeed, done two trials, blown the cylinder 186 cm on his first try and 152 cm on his second. The children decided Robbie should be listed only once, and were discussing which number to use.
|
Erin: |
If we use the number in the middle, both are inside the middle. There is some of each number in the middle. |
|
Andrea: |
You can count backwards from 186 to 152. (She writes down the numbers in descending order.) Now I can count how many numbers I just put down and then go halfway. I count down 17 from 186 and get 169. |
|
Sydney: |
People don't want Robbie to get a high or a low score, and the average seems more fair. |
|
Robbie: |
But I didn't get 169 as one of my distances. It wouldn't be true. It would be a lie! |
(based on Russell et al., in press)
Rather than insist that Robbie should have followed directions and taken only one measurement, the teacher recognizes an opportunity for the class to deal with a common issue in data interpretation, how to work with data that don't fit the predetermined format. In considering this issue, the children come up against the idea of the mean, further discussed below.
Often, once data have been collected, one may find that the method of collection has not provided data that address the original question, or that it has, but another question emerges as more significant or interesting. In their own data investigations, teachers must consider how to use pilot data to revise their questions and data collection procedures.
![]() The field of statistics offers a
variety of methods to explore and describe data.
The field of statistics offers a
variety of methods to explore and describe data.
Studying the shape of a data set and how data are spread has largely been neglected in school mathematics, but is critical to interpreting data (Shaughnessy, 1999). What does the shape of a data set indicate? Are the data clustered, spread out, symmetric, or skewed? Do most of the data cluster around a single value? Are they bimodal? flat? Where are there gaps? What is the range? Are there outliers? What does any of these characteristics indicate about the phenomenon represented?
Another core question arising from any data set---What is typical in this set?---introduces
particular statistical measures: mean, median, and mode. What does each tell about the data? What else is important to know about
the data in order to interpret their meaning?
These questions are considered by an elementary school class in the following scene.
Scene 17, from a fourth grade classroom: The children in the class measured their own heights and then collected heights from a first grade classroom. They met in groups to plan how to represent these two sets of data and created their representations. With a set of representations posted in the front of the room, the children discussed what they saw in the data:
|
Ilya: |
First graders are a lot smaller. The biggest first grader is 54 inches. |
|
Suzanne: |
A lot of first graders are near the heights of the smallest fourth graders. Not many have gotten up to the average height of a fourth grader in our class. Most fourth graders are 57 or 58 inches. |
|
Robert: |
The fourth graders have a larger range of heights than the first graders. . . . The fourth graders have a range of 14 numbers and the first graders have a range of 8 numbers. |
|
Mike: |
There are more first graders than fourth graders. There are 22 first graders and 21 fourth graders. |
|
Teacher: |
Does that tell you something you could say generally about all first graders and all fourth graders? |
|
Mike: |
No. |
|
Teacher: |
What about the other observations, that first graders aren't even as tall as an average fourth grader? Do you think that's typical or just these two classes? |
The discussion continues with children's observations.
|
Teacher: |
(toward the end of class) Can you give me a number that says how much taller a fourth grader is than a first grader, thinking about all the different ways you've thought about first grader heights and fourth grader heights? |
|
Diane: |
Ten inches, because the tallest fourth grader is 64 inches and the tallest first grader is 54 inches. |
|
Trudy: |
I think a first grader is about five inches smaller than a fourth grader. I found the median of fourth graders and first graders and I just subtracted. |
|
Suzanne: |
Five or four inches because the average first grader, the most common height, is 53 inches and the average fourth grader is 58 inches or 57 inches. |
|
Lincoln: |
I think to find the range between the first and fourth graders we need data from all the fourth grade classes and all the first grade classes. |
(based on Russell et al., in press)
Having collected and represented their data, these fourth graders tell their teacher what they see. But if she is
to understand their comments about range, overlap, clusters, median, and mode, she must know more about these concepts than
formulas convey---for example, what does the median communicate that is not given by the middle of the range?
(This particular question is important since many children confuse the two.)
Several of the children in Scene 16---Erin, Andrea, and Sydney---demonstrate
some appreciation of what the mean is and how one can find the mean of two numbers. However, Robbie's confusion is widely shared,
even among teachers: How can a value represent an entire set of data when that value does not appear in the data even once? To
develop a deeper understanding of what the mean represents, teachers might be given such problems as: Create a data set of eight
elements whose mean is 7. Create a second data set of eight elements, three above the mean and five below the mean.
After exploring shape, spread, and typicality, it is important to consider them in relation to one another. What does a single number represent and why is it useful? Within particular contexts, what else is important to know about a data set? Scene 17 illustrates children making reference to these characteristics to compare two data sets.
Data representation is a vibrant field offering a wide range of possibilities for data display. Although recognition of such possibilities is useful, fluency with those commonly used is imperative. Most teachers are already familiar with tables, bar graphs, and pie charts. But they should also be able to use line plots, stem-and-leaf plots, and box plots, among other methods of data display. By exploring the same data set in a variety of representations, teachers can consider how the latter communicate different aspects of the data and how one decides which form of representation to use for a given purpose. Specifically with regard to categorical data, how do different choices of category yield different views of the data?
One common source of confusion, for both children and teachers, is the difference between representations of value and representations of frequency (Bright & Friel, 1998; Konold & Higgins, in press). For example, given data on family size, one must distinguish between the number of members of each family versus the number of families of given sizes.
Outcomes that describe categories (gender, color preference, etc.) can be summarized by counts and plotted in bar graphs or pie charts. It is important to note that most of these summary statistics and descriptions of spread do not apply to categorical data.
![]() Data provide a selected view into
phenomena from which conclusions can be drawn.
Data provide a selected view into
phenomena from which conclusions can be drawn.
Once data have been collected, one must consider which conclusions can be drawn and how one communicates findings. Different sets of categories, modes of representation, and summary statistics give different views of the data and, thus, suggest different interpretations.
Issues of sampling and inference can be explored at this level in an informal way. Questions to be addressed include: Can a particular data set represent a larger population? What can data from one population tell you about another? For example, could the data about a single class generalize to all students of that age? Why or why not? What factors would need to be considered? What does it mean for a sample to be representative? How might a sample be biased? Why does the size of the sample matter?
These are questions that begin to arise in Scene 17. The teacher asks, "Does that tell you something you could say generally about all first graders and all fourth graders?" and again later, "Can you give me a number that says how much taller a fourth grader is than a first grader?" Lincoln (who earlier in the lesson expressed his sense that these particular first graders are exceptionally tall) suggests that, in order to make a general claim, they need to collect data from the other first and fourth grade classes. A teacher with a good understanding of sampling will be able to take advantage of this opening.
A related idea is that of variability. For example, in Scene 16, Robbie recorded two values for two attempts at "huff and puff." The teachers might ask, "If each of you were to try again, as Robbie did, would you get the same or a different number?"
Modern statistics is often thought of as a study of processes and the causes of variability. Students might study the time it takes to get through the lunch line, or classroom absences over a month, then consider causes of variability in the results they obtain. They might even suggest improvements to reduce variability.
Although establishing a relationship between two variables is not likely to be part of the elementary school curriculum, teachers should understand the idea of correlation and realize that correlation does not imply causality. Children with larger shoe sizes read better than those with smaller shoe sizes (there is a positive correlation between reading ability and shoe size among elementary school children), but the relationship is certainly not causal. For other variables, such as amount of sleep and academic performance, there may be causal links, but these can not be determined by simply tallying the sleep habits and grades of a few students.
Finally, data investigations are, by their very nature, open-ended. It may be possible to reach conclusions, but questions always remain. Furthermore, there are generally several correct routes to these conclusions. At the same time, it is important to dispel the common, naļve impression that "you can try anything you like and eventually something will work."
![]() The concepts of probability
provide ways of considering likelihood under conditions of uncertainty.
The concepts of probability
provide ways of considering likelihood under conditions of uncertainty.
Scene 18, from a second grade classroom: Groups of children are thinking about outcomes from rolling dice. As they engage in their experiment of rolling two dice and recording outcomes, they are surprised to notice that "7 kept winning." Before moving on to their experiment of rolling one die, the class discusses their predictions and most children expect that one number will predominate, just as the 7 had when using two dice. Then, after having collected data on their one-die rolls, the class meets to look at the data together and discuss their observations.
|
Alyssa: |
The numbers on the one-die chart came out almost the same with no number winning. On the two-dice chart, the 7 beat the other numbers. |
|
Teacher: |
When we made our predictions, many people thought 12 would win. Why do you think 12 has only two checks? |
|
Allison: |
You can only get 12 when you get two 6s and that's hard to get. |
|
Shelley: |
There's only one way to get a 12 and there is only one way to get a 2. |
As the class works on the number of ways to roll each number, Jonah observes, "It's like a football field," thinking about the yard lines. "The number of ways is the highest in the middle and it's smaller at each end." (based on Clark, 1996)
Children begin learning about probability by considering the likelihood of particular events in their daily lives (e.g., will it snow tomorrow?): impossible, certain, less likely, more likely. In Scene 18, children's experiments with dice introduce them to more precise concepts of probability: When rolling a single die, each outcome, 1 through 6, is equally likely. When rolling two dice, a 7 is more likely than a 12 because there are more ways to get a 7. In later years, the children will learn to assign numerical values to describe the likelihood of these events.
In order to teach them, teachers, too, must work on these ideas. Experiments with a balanced spinner can help them recognize that the probability of the spinner landing on a particular color is proportional to the area of that color. Experiments with coin tosses and dice can lead to an understanding that, given equally likely outcomes, the probability of a particular event is equal to the ratio of the number of outcomes defined by the event to the number of total possible outcomes.
In their work on probability, teachers must think through what randomness means. In 60 rolls of a die, each number will not necessarily appear exactly ten times. When flipping a coin five times, the result of HTTHH is no more likely than TTTTT.
The coin problem is based on the idea that one is starting with a fair coin which is tossed in a consistent manner. However, the type of problem with which one is usually confronted in applied work involves comparing observation to expectations. Thus, the problem could be turned around: Given that in five tosses we got the result TTTTT, should we look at the coin to see if it is fair before we make another bet?
A particularly challenging idea involves the difference between predicting an individual event and predicting a pattern of events. Teachers could work with simulation to explore this issue: When flipping a fair coin, how can one demonstrate that after a long run of heads, a tail is not "due"?
It must be emphasized that teachers should explore probabilistic concepts through physical simulation. The concepts of probability are difficult for almost everyone, and activities such as flipping coins, rolling dice, spinning spinners are the best means to learning. Later, even as teachers advance to computer simulation, physical experience should continue to be consulted.
In Chapter 2, it was recommended that prospective elementary teachers take at least 9 semester-hours of mathematics. Institutions will decide for themselves, preferably as collaborations between mathematics and education departments, how to structure the three courses to address the content described in this chapter. Some may choose to offer courses on number and operations, on geometry, and on algebra, respectively, selecting activities related to data to support content in each of these areas. Other institutions may choose other themes to define their courses, perhaps integrating content from number, algebra, geometry, and data into each of the three courses. In either case, content and methods courses should be coordinated.
Although research findings on teacher learning are still sparse, research on children's content learning can and should inform course design. For example, what is known about middle grades students' understanding of fractions has brought to light issues teachers urgently need to work on. (See, for example, Behr & Hiebert, 1988 or Carpenter et al., 1993.)
As content courses are designed, it should be kept in mind that teachers will not learn all the mathematics they
need to know in their undergraduate studies---even if, from their instructors' perspectives, the course content
has been covered. But if their undergraduate studies cultivate an interest in and capacity for mathematical activity, teachers
will be prepared to continue learning in the context of their everyday practice. Furthermore, having developed in their
undergraduate training a curiosity about mathematical ideas and an appreciation of mathematical pursuits, many more practicing
teachers will be interested in continuing their mathematics studies---an interest these institutions should be
prepared to address.
As for approaches to teaching mathematics to teachers, readers should be aware that several projects have been
using "records of practice"---videotapes of elementary school mathematics lessons, print cases that
illustrate children's mathematical thinking, samples of student work, teachers' reflections---as media of
instruction (Ball & Bass, 2000a; Ball & Cohen, 1999; Lampert & Ball, 1998; Barnett et al., 1994; Schifter et al.,
1999; Stein et al., 2000). These materials situate the mathematics in contexts resembling the elementary classrooms in which the
subject matter is to be employed. For example, many of the scenes presented in this chapter are suitable bases for mathematics
lessons for teachers. Thus, in courses taught by Magdalene Lampert, teachers take on for themselves the question posed by students
in Scene 5: Given the diagram below, illustrating how three pieces of cheese are distributed among 16 mice, how do we name the
portion each mouse gets?

Or, teachers could be asked to consider the question posed in Scene 3: Which features of the methods presented by
Henry and Michaela to solve 728 ![]() 34 reveal parallel lines of reasoning? Or again,
they might work through the solutions offered by the children depicted in Scenes 1 and 2 to reconcile the different strategies.
34 reveal parallel lines of reasoning? Or again,
they might work through the solutions offered by the children depicted in Scenes 1 and 2 to reconcile the different strategies.
By approaching content in this way, teachers who, themselves, have never had opportunities to work on the mathematics these children are addressing, now gain access to ideas that lay a foundation for more advanced work. On the other hand, for those who have already mastered this material, the cases provide a means to "decompress" it (in the language of Ball & Bass, 2000a), "to deconstruct . . . [their] own mathematical knowledge into less polished and final form, where elemental components are accessible and visible" (p. 98).
Useful as these "records of practice" might be to teachers learning mathematics, opportunities to work
on mathematical questions of their own---to become curious, to offer conjectures, to devise proofs, and to solve
problems---are indispensable. They need to become familiar with the pleasure of figuring things out, as well as
with the concomitant experiences of confusion and frustration, tolerating their discomfort long enough for things to fall into
place. If teachers never learn what this experience feels like, they won't have the gumption to allow their students to go through
it, either.
For the instructor, this kind of practice entails as much listening and questioning ---and
gumption---as telling or explaining. If teachers are to become mathematical thinkers, they must be given
opportunities to think---to go down blind alleys as well up productive avenues. The attentive instructor will
look for strengths in the ideas teachers offer, pose questions to help them analyze their errors, and point them toward
mathematically fruitful terrain.
For some instructors, teacher journal writing is an essential component of practice (Lampert & Ball, 1998).
There, teachers record their problem-solving process and write about the mathematics they are learning---their
new insights as well as the ideas with which they are struggling. Such writing allows teachers to consolidate their understanding
and, not incidentally, also provides a valuable assessment mechanism for the instructor.
This chapter began by observing that many prospective teachers have been less than successful mathematics students. Readers about to become their instructors may feel uneasy about how far back they'll have to reach to connect with these teachers. In going over the content described in this chapter, instructors may be tempted to start with topics in algebra because these seem respectably college-level. However, this is to begin at precisely the wrong place. If teachers have not had opportunities to make meaning for whole-number operations, to ground an understanding of why the operations work the way they do, ideas of generalization or function will elude them.
Taking on this work involves a different kind of mathematical challenge. The ideas teachers need to put together will seem so obvious to the mathematician as to be invisible. For example, why should anyone worry about why you can't additively decompose the divisor in a division problem? You can't do it because it doesn't work! The question seems absurd. But to the teachers who pose it, the question is compelling. The challenge to the mathematician is to figure out what makes this a substantive question and then to find a context in which teachers can think about it productively.
In one class where this issue arose, the teachers suggested that because making up word problems for particular
numerical expressions had proved helpful before, they would try it here: What if there were 12 candy bars to share among 6
children, 4 girls and 2 boys? Each child gets 2 candy bars, 12
![]() 6. But if you
decompose the divisor, 12 candy bars to share among 4 girls and 12 between 2 boys. . . . Suddenly, there were gasps and "oh's.''
"It's a different situation!'' "It doesn't make sense to add the number of candy bars each girl and each boy get.'' The
concrete context gave meaning to the symbols, offering access to the ideas of division. As one teacher later wrote, "Seeing
the division example as a word problem was [mind-]boggling. Suddenly the `why won't it work' appeared so clear'' (Schifter, 1993).
6. But if you
decompose the divisor, 12 candy bars to share among 4 girls and 12 between 2 boys. . . . Suddenly, there were gasps and "oh's.''
"It's a different situation!'' "It doesn't make sense to add the number of candy bars each girl and each boy get.'' The
concrete context gave meaning to the symbols, offering access to the ideas of division. As one teacher later wrote, "Seeing
the division example as a word problem was [mind-]boggling. Suddenly the `why won't it work' appeared so clear'' (Schifter, 1993).
In taking responsibility for the mathematics education of elementary teachers, mathematicians are invited, in effect, to re-enter the world of the naļve mathematical thinker. The recognition that the "unsophisticated" questions teachers pose do raise fundamental issues should inspire instructors to find contexts in which these can be addressed fruitfully. This means, at least initially, approaching the mathematics from an experientially based direction, rather than an abstract/deductive one. Isn't this the way each of us starts our individual journey into the world of mathematics?
Ball, D. L. (1989). Videotape of classroom lesson, September 19, 1989. Ann Arbor, MI: University of Michigan.
Ball, D. L. (1991). Research on teaching mathematics: Making subject matter knowledge part of the equation. In J. Brophy (Ed.) Advances in research on teaching: Teacher's subject matter knowledge and classroom instruction (Vol. 2, pp. 1-48). Greenwich, CT: JAI Press.
Ball, D. L. (1993). With an eye on the mathematical horizon: Dilemmas of teaching elementary school mathematics. Elementary School Journal, 93(4), 373-397.
Ball, D. L. & Bass, H. (2000a). Interweaving content and pedagogy in teaching and learning to teach: Knowing and using mathematics. In J. Boaler (Ed.), Multiple perspectives on the teaching and learning of mathematics (pp. 83-103). Greenwich, CT: JAI/Ablex.
Ball, D. L. & Bass, H. (2000b). Making believe: The collective construction of public mathematical knowledge in the elementary classroom. In D. Phillips (Ed.), Yearbook of the National Society for the Study of Education, constructivism in education (pp. 193-224). Chicago: University of Chicago Press.
Ball, D. L. & Cohen, D. K. (1999). Developing practice, developing practitioners. In L. Darling-Hammond & G. Sykes (Eds.), Teaching as the learning profession: Handbook of policy and practice. San Francisco: Jossey-Bass.
Ball, D. L. & Wilson, S. W. (1996). Integrity in teaching: Recognizing the fusion of the moral and the intellectual. American Educational Research Journal, 33, 155-192.
Barnett, C., Goldenstein, D., Jackson, B. (1994). Mathematics teaching cases: Fractions, decimals, ratios, & percents. Portsmouth, NH: Heinemann.
Bastable, V. & Schifter, D. (in press). Classroom stories: Examples of elementary students engaged in early algebra. In J. Kaput (Ed.). Employing children's natural powers to build algebraic reasoning in the content of elementary mathematics. Hillsdale, NJ: Lawrence Erlbaum Associates.
Bastable, V., Schifter, D. & Russell, S.J. (in press). Examining features of shape: Casebook. Parsippany, NJ: Dale Seymour Publications.
Battista, M. T. (1999). Fifth graders' enumeration of cubes in 3D arrays: Conceptual progress in an inquiry-based classroom. Journal for Research in Mathematics Education, 30(4), 417-448.
Battista, M. T. & Clements, D. H. (1998). Seeing solids and silhouettes. Menlo Park, CA: Dale Seymour Publications.
Behr, M. & Hiebert, J. (1988). Number concepts and operations in the middle grades. Reston, VA: National Council of Teachers of Mathematics.
Behr, M., Wachsmuth, I., & Post, T. (1985). Construct a sum: A measure of children's understanding of fraction size. Journal for Research in Mathematics Education, 16, 120-131.
Bright, G. W. & Friel, S. N. (1998). Graphical representations: Helping students interpret data. In S. P. Lajoie (Ed.), Reflections on statistics: Learning, teaching, and assessment in grades K-12. Mahwah, NJ: Lawrence Erlbaum.
Carpenter, T. P., Corbitt, M. K., Kepner, H. S., Lindquist, M. M., & Reys, R. E. (1981). Results from the Second Mathematics Assessment of the National Assessment of Educational Progress. Reston, VA: National Council of Teachers of Mathematics.
Carpenter, T. P., Fennema, E., & Romberg, T. (1993). Rational numbers: An integration of research. Hillsdale, NJ: Erlbaum.
Carpenter, T. P. & Levi, L. (1999). Developing conceptions of algebraic reasoning in the primary grades. Presented at the Annual Meeting of the American Educational Research Association, Montreal, Canada.
Carraher, D., Brizuela, B., & Schliemann, A., (2000). Bringing out the algebraic character of arithmetic: Instantiating variables in addition and subtraction. In T. Nakahara & M. Koyama (Eds.), Proceedings of the 24th Conference of the International Group of the Psychology of Mathematics Education (Vol 2., pp. 145-151). Hiroshima, Japan: Hiroshima University.
Clark, E. (1996). Patterns: Prediction and probability. In D. Schifter (Ed.). What's happening in math class? Envisioning new practices through teacher narratives (Vol. 1, pp. 14-17). New York: Teachers College Press.
Fitzgerald, W. & Shroyer, J. (1986). The mouse and the elephant. Palo Alto, CA: Addison Wesley.
Graeber, A. O. & Tanenhaus, E. (1993). Multiplication and division: From whole numbers to rational numbers. In D. T. Owens (Ed.), Research ideas for the classroom: Middle grades mathematics (pp. 99-117). New York: Macmillan.
Heaton, R. (1992). Who is minding the mathematics content? A case study of a fifth grade teacher. Elementary School Journal, 93(2), 153-162.
Heaton, R. (2000). Teaching mathematics to the new standards: Relearning the dance. New York: Teachers College Press.
Hiebert, J., Carpenter, T., Fennema, E., Fuson, K., Wearne, D. Murray, H., Olivier, A., & Human, P. (1997). Making sense: Teaching and learning mathematics with understanding. Portsmouth, NH: Heinemann.
Kaput, J. (Ed.). (in press). Employing children's natural powers to build algebraic reasoning in the content of elementary mathematics. Hillsdale, NJ: Lawrence Erlbaum Associates.
Konold, C. & Higgins, T.L. (in press). Statistics and data analysis. In J. Kilpatrick, W. G. Martin, & D. Schifter (Eds.), Research companion to the Principles and Standards of School Mathematics. Reston, VA: National Council of Teachers of Mathematics.
Lampert, M. & Ball, D. L. (1998). Teaching, multimedia, and mathematics: Investigations of real practice. New York: Teachers College Press.
Ma, L. (1999). Knowing and teaching elementary mathematics: Teachers' understanding of fundamental mathematics in China and the United States. Hillsdale, NJ: Lawrence Erlbaum Associates.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
Russell, S. J., Schifter, D. & Bastable, V. (in press). Working with data: Casebook and facilitator's guide. Parsippany, NJ: Dale Seymour Publications.
Russell, S. J., Smith, D. A., Storeygard, J., & Murray, M. (1999). Relearning to teach arithmetic (videotapes and study guide). Parsippany, NJ: Dale Seymour Publications.
Schifter, D. (1993). Mathematics process as mathematics content: A course for teachers. Journal of Mathematical Behavior, 12(3), 271-283.
Schifter, D., Bastable, V., & Russell, S. J. (in press-a). Measuring space in one, two, and three dimensions: Casebook. Parsippany, NJ: Dale Seymour Publications.
Schifter, D., Bastable, V. Russell, S. J. (with Yaffee, L., Lester, J. B., & Cohen, S.) (1999a). Making meaning for operations: Casebook. Parsippany, NJ: Dale Seymour Publications.
Schifter, D., Bastable, V. Russell, S. J. (with Lester, J. B., Davenport, L. R., Yaffee, L. & Cohen, S.) (1999b). Building a system of tens: Facilitator's guide. Parsippany, NJ: Dale Seymour Publications.
Schifter, D., Bastable, V., Russell, S. J. (with Cohen, S., Lester, J. B., & Yaffee, L.) (1999c). Building a system of tens: Casebook. Parsippany, NJ: Dale Seymour Publications.
Schifter, D., & Fosnot, C. T. (1993). Reconstructing mathematics education: Stories of teachers meeting the challenge of reform. New York: Teachers College Press.
Shaughnessy, M. (1999). Research and assessment issues in the teaching and learning of probability and statistics: What questions might we be asking? Presented to the Research Presession of the 1999 Annual Meeting of the National Council of Teachers of Mathematics, San Francisco.
Simon, M. A., & Blume, G. W. (1994). Building and understanding multiplicative relationships. Journal for Research in Mathematics Education, 25(5), 472-494.
Stein, M. K., Smith, M. S., Henningsen, M. A., & Silver, E. A. (2000). Implementing standards-based mathematics instruction: A casebook for professional development. New York: Teachers College Press.
Thompson, P. W. (1993). Quantitative reasoning, complexity, and additive structures. Educational Studies in Mathematics, 25(3), 165-208.
Tierney, C., Ogonowski, M., Rubin, A., & Russell, S. J. (1998). Different shapes, equal pieces. Menlo Park, CA: Dale Seymour Publications.
Usiskin, Z. (1987). Resolving the continuing dilemmas in school geometry. In M. M. Lindquist (Ed.), Learning and teaching geometry, K-12, 1987 Yearbook of the National Council of Teachers of Mathematics (pp. 17-31). Reston, VA: National Council of Teachers of Mathematics.
Usiskin, Z. (1988). Conceptions of school algebra and uses of variables. In A. Coxford & A. Shulte (Eds.), The ideas of algebra, 1988 Yearbook of the National Council of Teachers of Mathematics (pp. 8-19). Reston, VA: National Council of Teachers of Mathematics.
van Hiele, P. (1986). Structure and insight. Orlando, FL: Academic Press.