
 |
 |
![]()
 |
Working Group Session # 18 - Joan Ferrini-Mundy and Gail Burrill
|
Despite the substantial mathematical preparation of many of the nation’s teachers of secondary school algebra, data continue to indicate that secondary school students have difficulties both in understanding the concepts of algebra and in performing the procedures that are central to algebra. In this presentation we focus on three areas:
| Highlights of the secondary school algebra landscape | |
| Algebra knowledge for teaching | |
| Issues in the undergraduate preparation of mathematics teachers |
Within the past decade, much about the status of school algebra has changed dramatically. In general, this area, which was for many years available only to the college-bound, and in its advanced forms, only for those headed toward mathematics-based careers, is now seen as crucial preparation for all students. The 2000 National Assessment of Educational Progress (NAEP)[1] showed that 94% of students in grade 12 report having taken Algebra One. At the same time, 80% of students report having taken Algebra Two, an increase from the 56% who reported this in 1990. Professional organizations, authors of instructional materials, mathematicians and mathematics educators, and policy makers and teachers in the K-12 community alike are supporting the idea of “algebra for all,” and the results are becoming visible in course enrollments.
A second element in the K-12 landscape concerning algebra is that school algebra in the United States is viewed as encompassing a wider range of topics than it did decades ago, where the emphasis was primarily on the structural aspects of the subject – properties of number systems and their extensions into algebraic systems, and on fluency in the procedures of algebra. Currently, a wider view of the subject is represented in key policy documents. And, at the same time, current policy recommendations call for algebra and algebraic ideas to be introduced into the curriculum much earlier than ever before. For example, the proposed Mathematics Framework for NAEP 2005[2] includes the following areas within the algebra category:
| Patterns, relations, and functions | |
| Algebraic representations | |
| Variables, expressions, and operations | |
| Equations and inequalities |
These areas would be tested at grades four, eight, and twelve. Similarly, the framework that has been developed for achievement testing at grades four, eight, and twelve in TIMSS 2003[3] organizes algebra as follows:
| Patterns | |
| Algebraic expressions | |
| Equations and formulas | |
| Relationships |
Finally, the National Council of Teachers of Mathematics (NCTM), in its
Principles and Standards for School Mathematics[4], includes an
Algebra Standard:
Instructional programs from pre-kindergarten through grade 12 should enable all students to:
| Understand patterns, relations, and functions; | |
| Represent and analyze mathematical situations and structures using algebraic symbols; | |
| Use mathematical models to represent and understand quantitative relationships; | |
| Analyze change in various contexts. (p. 37) |
These various categorizations and ways of organizing the content of algebra are indicative of the disagreements and varied perspectives that mathematicians, mathematics educators, and teachers have taken relative to the specification of the “content” of school algebra. This is as area where there are differences of opinion that some have described as different “perspectives” on school algebra. In 1995, the NCTM Algebra Working Group[5] offered yet another set of perspectives:
| Functions and relations | |
| Modeling | |
| Structure | |
| Language and representation |
Chazan[6] summarized the various perspectives as the following:
| Algebra as a generalization of arithmetic | |
| Theory of equations | |
| Mathematical models for nonmathematical situations | |
| Functions | |
| Expressions | |
| Abstract algebra/structures. |
The previous remarks presumably help to establish that the landscape of school algebra is a dynamic one, with a variety of components and shifting elements. At the same time, the business of preparing teachers to teach in the nation’s schools and of providing ongoing professional development to support teachers in their work continues. NCTM’s Principles and Standards, in the Teaching Principle, points at the complex mix of knowledge required in teaching: “Effective mathematics teaching requires understanding what students know and need to learn and then challenging and supporting them to learn it well” (p. 11).
The questions of “What is the mathematical knowledge teachers need to know to teach well?” and “How can teachers develop the mathematical knowledge they need to teach well?” are of great interest to researchers, teacher educators, and mathematicians. These questions were used to frame a workshop at the National Research Council in 1999[7]; The Mathematical Education of Teachers volumes propose answers to these questions. In the MET report, the authors are clear about the kind of mathematical knowledge expected of high school teachers: “a deep understanding of the fundamental mathematical ideas in the grades 9-12 curricula…” (p. 122).
A number of researchers are interested in questions about what mathematical knowledge is required for teaching. Deborah Ball and Hyman Bass[8] at the University of Michigan have been interested in the question of the mathematical knowledge entailed by teaching for several years. They have described mathematics teaching, along with other professions such as engineering, as a “mathematically intensive” profession, and have talked about “pedagogically useful mathematical knowledge.” They have studied elementary school mathematics teaching through the analysis of videotapes and other artifacts of teaching, and have proposed a number of useful categories of mathematical knowledge for teaching.
At Michigan State University, a group of faculty are examining related questions in a study of algebra knowledge for teaching at the secondary school level.[9] The fundamental question in this effort is: What knowledge of algebra for teaching (mathematical knowledge, beliefs, dispositions and conceptions of mathematics) do secondary school teachers of algebra draw upon to support their instruction? The project is intended to produce a framework describing algebra knowledge for teaching and prototype tasks or tools to assess teacher knowledge.
The area of mathematical knowledge for teaching has begun to attract other national attention. In fact, it was identified as a priority area of research in the draft report of the RAND Mathematics Study Panel[10], one of three priority areas for research. Another is algebra teaching and learning. The report noted: “…overarching goal of our program of research is to achieve mathematical proficiency for all students…the first area [selected for intense, programmatic focus] is algebra…our third priority is knowledge needed for teaching…” (p. 12-13).
It is unclear how college and university departments of mathematics can best make changes that will improve the mathematical preparation of teachers. It may be that core mathematics major courses can be redesigned to help future teachers make insightful connections between the advanced mathematics they are learning and the high school mathematics they are teaching. In any case, developing more clarity about the mathematical demands of secondary school teaching seems a crucial step as mathematics departments work to improve the education of teachers.
To enable us to collectively focus on issues about algebra teaching, we have prepared six "algebra teaching situations" for small group discussion. These are drawn from various mathematics education literature as well as the experiences of teachers and teacher educators. We ask that you work, in small groups, to focus on the following three questions:
| What does the teacher need to know about algebra? | |
| What does the teacher need to know about students as learners of algebra? | |
| Where would teachers best learn what they need to know in 1 and 2? |
A. A teacher of 7th grade pre-algebra notices that several of her students,
when asked to “simplify 2x + 5 + 3x – 7”, do the
following:
| 2x + 5 + 3x – 7 = 0 |
| 5x – 2 = 0 |
| 5x = 2 |
| x = 2/5 |
B. An algebra teacher has taught his students the rule: “When you multiply, you add exponents. When you divide, you subtract.” Several of his students make the following error:
| 32 x 33 = 95 |
How might the teachers think about these responses?
An algebra one textbook contains the following homework problem. This comes
after a lesson about solving equations in one variable by considering the
expression on each side of the equal sign as a function. A student has come in
after school to see his teacher, the student has no idea how to approach the
homework problem.
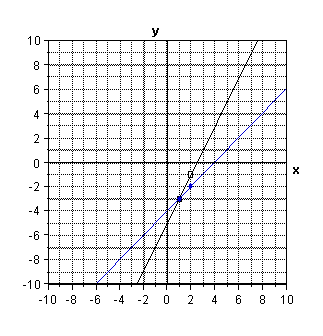
Problem 32. Below, Tanya and Andy solve 2x – 5 = - x + 4 using graphs.
Does each method give a correct solution? Explain.
|
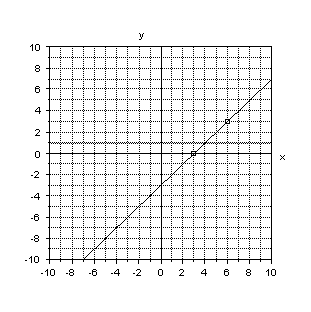 |
|
 |
An eighth-grade algebra one teacher is planning to introduce the concept of slope. She has assigned the section of the textbook that introduces slope to her students as homework reading to be done the night before her lesson. The reading is four pages long, and includes the following descriptions of slope within the 4 pages:
|
One of the homework problems the teacher would like to assign is:
| Use the concept of slope to decide whether the points (1,1), (0,-3),
(5,12) lie on the same line. Explain your thinking and include a diagram. |
She wants to plan her lesson so that her students will be able to coordinate what they have seen in the reading and be successful with the homework problem. Has the text introduction provided the students with adequate background?

An eighth grade teacher using an integrated mathematics series is concerned about an upcoming eighth-grade state assessment that will include algebra. In looking at the test framework, she finds the following sample problem[13] and solution:
|
Jennifer Made a 100-mile trip by car on a road that was being
repaired. She began at noon and arrived at her destination at
3:30pm. Because of the construction zone, she was able to average only
20 mph for a long stretch in the middle of the trip. The rest of
the time she drove 70 mph. How long was the construction zone?
Solution to the Road Trip Let x denote the number of miles of construction (during which Jennifer drove 20 mph); then100 - x will be the number of miles when she drove 70 mph. The total time of the trip, 3.5 hours, consists of the time she was driving 20 mph, namely x / 20, plus the time she was driving 70 mph, namely (100 - x) / 70. Thus:
So the length of the construction zone is 58 miles. |
She is concerned because her students have been using mainly tables and graphs to work on problems like this.
A first year teacher of 10th and 11th graders in an algebra course introduces the absolute value function by explaining the notation f(x) and showing students the graph, f(x) = | x |.
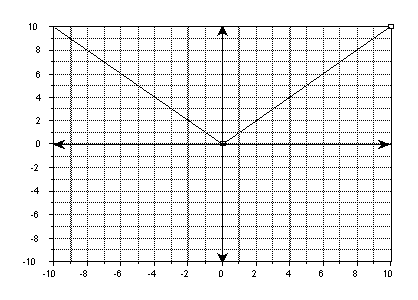
A 10th grader who has had a geometry course asks: "Is this the way you can write equations for angles?"
![]()
[1] Silver, Edward A. and Patricia Ann Kennedy (Eds.). (2000). Results from the Seventh Mathematics Assessment of the National Assessment of Educational Progress. National Council of Teachers of Mathematics. Reston, VA.
[2] National Assessment Governing Board. (December, 2001). Mathematics Framework for 2005. National Assessment of Educational Progress. Pre-Publication Edition. Washington, D.C.: p. 31-33.
[3] Mullis, Ina V.S., Michael O. Martin, Teresa A. Smith, et al. (September, 2001). TIMSS Assessment Frameworks and Specifications 2003. International Study Center, Lynch School of Education, Boston College: p.14.
[4] National Council of Teachers of Mathematics. (2000.) Principles and Standards for School Mathematics. National Council of Teachers of Mathematics, Reston, VA.: p. 37.
[5] National Research Council. (1998). The nature and role of algebra in the K-14 curriculum: Proceedings of a national symposium. Washington, D.C.: National Academy Press.
[6] Chazan, Daniel. (2000). Beyond Formulas in Mathematics and Teaching: Dynamics of the High School Algebra Classroom. Teachers College Press, Columbia University, New York, NY.
[7] National Research Council. (2001). Knowing and Learning Mathematics for Teaching. Washington, D.C.: National Academy Press.
[8] See, for example, Ball, D. L., & Bass, H. (2000). Interweaving Content and Pedagogy in Teaching and Learning to Teach: Knowing and Using Mathematics. In J. Boaler (Ed.), Multiple Perspectives on the Teaching and Learning of Mathematics (pp. 83-104). Westport CT: Ablex.
[9] NSF ROLE Program, Award no. REC-0106709, A Study of Algebra Knowledge for Teaching. PI Joan Ferrini-Mundy; Co-PIs Sharon Senk and Daniel Chazan.
[10] RAND Mathematics Study Panel (March, 2002). Mathematics proficiency for all students: Toward a strategic research and development program in mathematics education. Draft report, prepared for the Office of Educational Research and Improvement. http://www.rand.org/multi/achievementforall/math/submathdraft.html
[11] Adapted from Wagner, S. & Parker, S. (1993). Advancing Algebra. In P.Wilson, Ed., Research Ideas for the Classroom: High School Mathematics. New York: MacMillan.
[12] Adapted from an algebra one textbook; complete reference to follow.