
 |
 |
![]()
 |
Working Group Session # 2 - Deborah Schifter
|
For this session, I was asked to introduce Summit participants to Developing Mathematical Ideas. To do so, I provided an overview of these materials and, as illustration, worked through the treatment of one idea in particular—that of the area of a triangle. But this session had an additional goal: to attend to the insights, as well as the questions and confusions, that teachers bring to the development of this idea.
Developing Mathematical Ideas (DMI) is a professional development curriculum designed to help teachers think through the major ideas of K-7 mathematics and examine how children develop those ideas. At the heart of the materials are sets of classroom cases exhibiting student thinking as described by their teachers. In addition to case discussions, the curriculum offers teachers opportunities: to explore mathematics in lessons led by facilitators; to share and discuss the work of their own students; to plan, conduct, and then analyze mathematics interviews of their own students; to view and discuss videotapes of mathematics classrooms and mathematics interviews; to write their own classroom episodes; to analyze lessons taken from innovative elementary mathematics curricula; and, finally, to read overviews of related research. DMI seminars bring together teachers from kindergarten through middle grades to:
| learn mathematics content, | |
| learn to identify key mathematical ideas with which their students are grappling, | |
| learn to recognize and extend the power and complexity of student thinking, | |
| learn how core mathematical ideas develop across the grades, | |
| learn how to continue learning about children and mathematics. |
Materials for two seminars, on themes of Number and Operations, were published in 1999. Under production are three
additional modules. Each module is designed for eight three-hour sessions.
| Number and Operations, Part 1: Building a System of Tens. Participants explore the base-ten structure of the
number system, consider how that structure is exploited in multidigit computational procedures, and examine how basic concepts of
whole numbers reappear when working with decimals. | |
| Number and Operations, Part 2: Making Meaning for Operations. Participants examine the actions and situations
modeled by the four basic operations. The seminar begins with a view of young children's counting strategies as they encounter
word problems, moves to an examination of the four basic operations on whole numbers, and revisits the operations in the context
of rational numbers. | |
| Geometry: Examining Features of Shape. Participants investigate aspects of 2D and 3D shapes, develop geometric
vocabulary, and explore both definitions and properties of geometric objects. The seminar includes a study of angle, similarity,
congruence, and the relationships between 3D objects and their 2D representations. (Available December 2001) | |
| Geometry: Measuring Space in One, Two and Three Dimensions. Participants examine different attributes of size,
develop facility in composing and decomposing shapes, and apply these skills to make sense of formulas for area and volume. They
also explore the concepts of length, area, and volume, as well as their complex inter-relationships. (Available November 2001) | |
| Working with Data. Participants explore the collection, representation, description, and interpretation of data. They learn what various graphs and statistical measures show about features of the data, study how to summarize data when comparing groups, and consider whether the data gathered provide insight into the questions that led to their collection. (Available March 2002) |
Materials for Participants: The Casebooks
Each seminar is built around a casebook containing 25 to 30 cases, the cases grouped into seven chapters, each tracking a
particular mathematical theme from kindergarten through grade six. Casebooks begin with an overview of the seminar, and each
chapter with an introduction intended to orient the reader to the major theme of the cases to follow. The casebooks conclude with
an accessible, jargon-free essay entitled Highlights of Related Research: having worked through seven sets of cases to explore
children's mathematical thinking as seen by their teachers and set in classroom contexts, seminar participants now consider these
same issues from a research perspective.
Materials for Facilitators
The DMI Facilitator’s Guides include detailed agendas for each session. Other components are intended to help
facilitators: identify particular strategies useful in leading case discussions and mathematics activities; plan seminar sessions;
understand the major ideas to be explored in each session; and think through issues of teacher change.
The DMI Video Cases show students in a wide variety of classroom settings and with children and teachers of different
races and ethnic groups. While written cases allow users to examine student thinking at their own pace, returning, if necessary,
to ponder and analyze particular passages, video offers opportunities to listen to real student voices in real time and provides
rich images of classrooms organized around student thinking.
DMI Leadership Institutes
The DMI Leadership Institute Program is designed for teams of staff developers, teacher-educators, teacher-leaders and others who
support teachers' professional development in mathematics K-7. Institute participants work in a community of peers to inquire into
the goals of professional development for elementary and middle school mathematics, reflect on the kinds
of structures and activities that can support those goals, and become familiar with DMI as a tool to advance the mathematics
education agenda at their sites. Two levels of DMI Leadership Institutes are offered. DMIL1, based on Building a System of Tens
and Making Meaning for Operations, is appropriate for educators new to the DMI materials. DMIL2 builds on the work of DMIL1 and
also includes opportunities for participants to become familiar with the geometry, measurement, and data modules.
For More Information
To order materials from Dale Seymour Publishers, call (800) 321-3106.
To find out about DMI Leadership Institutes, call (413) 538-2063
or e-mail smt-dmiinfo@mtholyoke.edu.
To check out the DMI web site, go to http://www.edc.org/LTT/CDT/DMIcur.html.
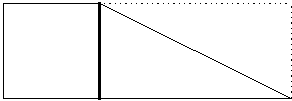
I have been teaching mathematics to teachers since 1988. A particular issue that has, at times, stymied me is the difficulty some teachers have had in interpreting the diagram below.
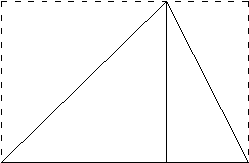
Often, teachers could tell me that the two right triangles were each half of a corresponding rectangle, but they did not see how
they could then conclude that the area of the entire acute triangle was half that of the full rectangle. It was hard for me to see
what was opaque about the ideas in this so seemingly transparent diagram. I knew that some of the teachers who struggled with this
issue were perfectly comfortable with the distributive property when thinking about numbers and counting objects. The issue here
must have had to do with reasoning geometrically, I conjectured.
The formula for the area of a triangle (as well as those for the rectangle, parallelogram, and trapezoid) is one of the issues
taken up in the module, Measuring Space in One, Two, and Three Dimensions. In designing the module, I wanted to step
back far enough so that, when teachers came to it, they would be able to use diagrams like this one to construct proofs for area
formulas. In this MET session, I took participants through a series of activities taken from the module.
A Sample of Activities from Measuring Space in One, Two, and Three Dimensions
1. Mathematics Assignment: Crazy Cakes. A sheet distributed to Summit participants provided a variety of polygonal shapes (crazy
cakes) with the instructions to cut each into two regions of equal area. (The activity was taken from Tierney, Ogonowski, Rubin,
& Russell, Different Shapes, Equal Pieces, a grade 4 unit of Investigations in Number, Data, and Space.) For
example, given this shape:
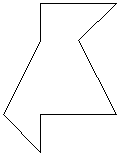
one can find several ways to cut, with different methods of justification:
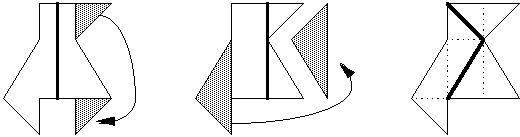
2. Video Case: Crazy Cakes. Summit participants then viewed a video clip of fourth-grade students working on the same mathematics activity. In the video, fourth grader, Aneschka, divides the cake as shown, and labels each piece “1” or “2”according to whether it goes to person 1 or person 2.
Her partner doesn’t understand what Aneschka has done. Her partner, Kayla, says there’s a problem because the two triangles labeled “1” are different sizes. [Summit participants viewing this tape paraphrased Aneschka’s method for cutting the cake into regions of equal area and articulated where Kayla’s confusion lay.]
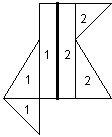
In a second video clip, another fourth grader, Lisa, presents her ideas about cutting this shape:
As shown below, she has divided the figure into a square and a triangle, each half the original shape. She explains that she imagined a triangle of the same size fitted on top of the triangle to make a rectangle. She reasons that both the square and the triangle are half the area of the same, resulting rectangle, and so are equal in area to one another.
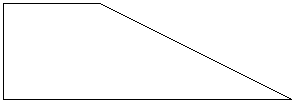
3. Mathematics Activity: Area of a Triangle. A worksheet distributed to Summit participants is designed to help teachers move from these exercises to consider how, given some measures of a figure, others could be determined. For example, “Given that the area of the original trapezoid, above, is 32 square units, What is the area of the square? What is the length of the sides of the square? What is the area of the triangle? What is the length of its base? its height?” The set of questions on this activity sheet next explores the relationship between the area of a triangle and that of a suitably constructed rectangle. “If the rectangle below has dimensions of 8 units by 4 units, find the area of the triangle and explain your method.”

The last question on the worksheet asks teachers to investigate the truth of this general statement: For every
triangle, a rectangle can be drawn around it so that the area of the rectangle is exactly double the area of the triangle.
4. Print Case: “Area of Triangles.” Summit participants were presented with an overview of a case written by a teacher of a
third- and fourth-grade combination class. The case describes three lessons in which children explore the area of a triangle, each
successive lesson raising the level of generality.
DMI facilitator’s guides contain a section, called “Maxine’s Journal,” in which a fictional facilitator reflects on each of the seminar sessions. Although Maxine is invented, the events she describes are not. Indeed, her narratives are based on what took place in seminars that piloted the DMI materials.
At the MET Summit session, participants were given two sections of Maxine’s Journal to read, one describing seminar teachers’ engagement with the Mathematics Activity: Area of a Triangle; another, following teachers’ reading of the case, “Area of Triangles.” Summit participants made a number of points about the work of teachers in Maxine’s seminar.
|
The Crazy Cakes activities provided many teachers a way to think about decomposing area and comparing regions, a
skill they called upon to reason about the area of a triangle. | |
|
Some teachers’ confusion paralleled that of Kayla, the fourth grader in the video. That is, they could see that
an isosceles triangle drawn within a rectangle has half the area of the rectangle. However, when looking at a scalene triangle,
they were so distracted by its lack of symmetry, they had difficulty seeing that the area within the triangle is equal to the area
without. (This is not to say that the teachers stop here and cannot reason through the problems. Rather, this is a hurdle they
must work through.) | |
|
Quite a few teachers chose to count squares on a grid to find the area of a triangle. One Summit participant
observed that these teachers now have two ways to think about the area of a shape, one based on counting squares, the other based
on comparing regions. It is to their credit that they are now working to reconcile the two methods, to demonstrate to themselves
that the methods are equivalent. Most participants said they were pleased to see teachers taking the initiative to make the
mathematics make sense to them. | |
|
Reading the case gave teachers an additional opportunity to reconcile the two methods, since the children, too,
were counting squares and comparing regions. | |
|
Summit participants were struck by the teachers’ comments about their own middle- and high-school experiences:
“I bet my teachers didn’t understand it,” and “Why did the math authorities [sic] decide they would just give us the
formula without understanding it?” Participants commented that perhaps, back then, these teachers (then adolescents) were
provided an explanation but weren’t open to hearing it. However, the point was made that at the beginning of this DMI seminar,
these teachers most likely would still not have been ready to follow such an explanation. The module was designed to cultivate a
set of skills precisely in order to help teachers make sense of the proof for the area formula of a triangle. | |
|
Summit participants wanted to know whether all of the teachers in the pilot class finally understood the area
formula for a triangle. I said that all but one did. That one teacher was able to compare the area of a triangle to a
corresponding rectangle, but had trouble seeing how the formula connected. I believe this teacher didn’t know how to think about
variables (“What do b and h have to do with the area of a rectangle—it’s l times w?”) and so couldn’t translate the
ideas into the language of a formula. | |
|
One participant was curious about how the teachers extended their thinking to consider the area of an obtuse triangle. I told them for that issue was addressed in the next section of Maxine’s Journal and there was neither the time nor the appropriate materials to deal with that question here. |