
 |
 |
![]()
Contents |
Committee | Preface
| Ch 1 | Ch 2 |
Intro to Ch 3-9 | Ch 3
| Ch 4 | Ch 5 |
Ch 6 | Refs for Part 1
| Other Reports | Ch 7
| Ch 8 | Ch 9
The more sophisticated content of middle grades![]() mathematics necessitates that mathematics specialists teach in
these grades and that these specialists have a well-developed understanding of the mathematics they teach. The mathematics
expected of middle grades students builds on but is qualitatively different from the mathematics of the earlier grades. Students,
for example, are expected to be able to operate with understanding on rational numbers; measure not only geometric shapes but in a
variety of situations; develop understanding of similarity, congruence, and symmetry; mentally operate on geometric shapes;
recognize and represent linear relationships with tables, graphs, and equations; gather, appropriately represent, and interpret
simple data sets; and apply basic concepts of probability to measure uncertainty. Students must develop the ability to recognize
situations in which it is appropriate to use ratios rather than differences to make mathematical comparisons. They should be
helped to see the connections that exist among the mathematical topics they learn.
mathematics necessitates that mathematics specialists teach in
these grades and that these specialists have a well-developed understanding of the mathematics they teach. The mathematics
expected of middle grades students builds on but is qualitatively different from the mathematics of the earlier grades. Students,
for example, are expected to be able to operate with understanding on rational numbers; measure not only geometric shapes but in a
variety of situations; develop understanding of similarity, congruence, and symmetry; mentally operate on geometric shapes;
recognize and represent linear relationships with tables, graphs, and equations; gather, appropriately represent, and interpret
simple data sets; and apply basic concepts of probability to measure uncertainty. Students must develop the ability to recognize
situations in which it is appropriate to use ratios rather than differences to make mathematical comparisons. They should be
helped to see the connections that exist among the mathematical topics they learn.
Teachers of middle grades students must be able to build on their students' earlier mathematics learning and develop a broad set of new understandings and skills to help their students meet these more sophisticated goals. New curricula now being adopted in many districts reflect these goals and assume a high level of understanding on the part of the teacher. Teaching middle grades mathematics requires preparation different from, not simply less than, preparation for teaching high school mathematics, and certainly reflecting more depth than that needed by teachers of earlier grades (described in the previous chapter). Too few teacher preparation programs offer preparation targeted for teachers of the middle grades. In many cases these teachers have been prepared to teach elementary school mathematics and lack the broader background needed to teach the more advanced mathematics of the middle grades.
Recommendation 2 of Chapter 2 advocates a program of at least 21 semester-hours of mathematics for prospective mathematics teachers of these grades. Two types of courses should be included. First, courses must be designed that will lead prospective teachers to develop a deep understanding of the mathematics they will be teaching. The design of this coursework, approximately 12 semester-hours, is the focus of this chapter. Some of this coursework could overlap with coursework for K-4 teachers, particularly that concerning fundamental ideas, such as place value, that extend from whole numbers to decimals.
Second, courses are needed that will strengthen these prospective teachers' own knowledge of mathematics and broaden their understanding of mathematical connections between one educational level and the next, connections between elementary and middle grades as well as between middle grades and high school. This second type of coursework should be carefully selected from the options offered by the department, and would require a precalculus or college algebra background. One semester of calculus could be part of this second group of courses if there is (or could be designed) a calculus course that focuses on concepts and applications, as opposed to the traditional course offered to mathematics majors and engineers.
Number theory and discrete mathematics can offer teachers an opportunity to explore in depth many of the topics they will teach. A history of mathematics course can provide middle grades teachers with an understanding of the background and historical development of many topics in the middle grades curriculum. A mathematical modeling course, depending on the level and substance of the course, can provide prospective teachers with understanding of the ways in which mathematics can be applied. If the prospective teachers are likely to teach algebra, coursework in linear algebra and modern algebra would be appropriate. If, in addition, the teachers might be expected to teach a full-year course in geometry, then they should have the same geometry coursework as prospective secondary teachers. These options would most likely require more than 21 semester-hours.
Making sense of mathematics should be a cross-cutting theme throughout K-12 mathematics instruction and in courses for prospective teachers. For many prospective teachers learning mathematics has meant only learning its procedures and, they may, in fact, have been rewarded with high grades in mathematics for their fluency in using procedures. Although procedural fluency is necessary, it is not an adequate foundation for teaching mathematics. An orientation towards making sense of mathematics must be considered fundamental both to learning and to teaching mathematics.
Problems involving proportionality permeate middle grades curricula, and therefore provide a focus for much of the content discussed here. Proportions occur, for example, in arithmetic tasks involving ratios and percents, in geometry tasks involving similarity, in algebra tasks involving linearity, and in tasks requiring the assignment of a probability to an event. Many prospective teachers have had only a one- or two-day encounter with proportions in their own schooling. That encounter may have involved only what are often called missing-value problems intended to be solved by applying a particular procedure: setting up a proportion and cross-multiplying to find an unknown value. If they are limited to this understanding teachers may fail to recognize when tasks are proportional in nature and so will miss opportunities to help their future students develop ability to reason appropriately with proportions. Proportional reasoning is a psychologically and mathematically sophisticated form of reasoning based on intuitive preschool experiences and developed in school through appropriate experiences (Sowder et al., 1998). For example, this problem requires proportional reasoning, but goes well beyond the standard matching of two ratios and cross-multiplying:
In a certain town, the demand for rental units was analyzed, and it was determined that, to meet the community's needs, builders would be required to build apartments in the following way: Every time they build three single-bedroom apartments, they should build four 2-bedroom apartments and one 3-bedroom apartment. Suppose a builder is planning to build a large apartment complex counting between 35 and 45 apartments. How many 1-bedroom apartments, 2-bedroom apartments, and 3-bedroom apartments would the apartment building contain? (Lamon, 1993, p. 44)
Another theme of middle school mathematics is that of variables and relations, and especially the multiple equivalent representations of relations among variables. Through their work on variables and relations students begin to develop an understanding of functions and of the power of symbols. This initial work sets the stage for further work in mathematics. Teachers need to foster algebraic thinking (e.g., recognizing patterns and finding governing rules, being able to think about quantities without necessarily attaching values, and being able to reverse operations [Driscoll, 1999]) in the early grades and then more particularly in the middle grades. To do so they need to recognize what types of tasks lend themselves to helping their students begin to reason about variables, relations, and functions, tasks involving such activities as making tables, searching for patterns, graphing, and generalizing.
Explaining one's reasoning in carrying out mathematical tasks is difficult for most adults who have never been required to do so in previous mathematics coursework. But this ability is fundamental to successful instruction and should be required in courses designed for this population. When reasoning, explaining, and sense-making are emphasized in teacher preparation courses, prospective teachers are more likely to assimilate these ways of thinking and communicating and apply them to their own learning, and they will be better prepared to model these aspects of mathematics when they begin teaching.
The remainder of this chapter discusses four content areas of mathematics in terms of developing prospective teachers' understanding. This understanding is dependent on reasoning, explaining, and sense-making. Topics in these four areas are found throughout the K-12 curriculum but vary in emphasis at each of level of schooling. This chapter focuses on the fundamental concepts and skills needed to teach mathematics well in the middle grades.
Coursework for prospective middle grades teachers should lead them to:
| Understand and be able to explain the mathematics that underlies the procedures used for operating on whole numbers and
rational numbers. | |
| Understand and be able to explain the distinctions among whole numbers, integers, rational numbers, and real numbers, how they
are placed on the number line, and how field axioms hold or do not hold depending on the types of numbers being used. | |
| Convert easily among fractions, decimals, and percents. | |
| Demonstrate facility in using number and operation properties, including mental computation and computational estimation. | |
| Understand and be able to explain fundamental ideas of number theory as they apply to middle school mathematics. | |
| Make sense of large and small numbers and use scientific notation. | |
| Apply proportions appropriately and provide explanations. |
Number continues to be a focus of mathematics in the middle grades, but there is a shift in these grades from work with whole numbers to work with rational numbers. By the time students complete the middle grades, they should be able to recognize which arithmetic operation or operations can be used appropriately to solve a particular problem and to carry out the procedures to obtain a correct answer. They also should be able to use numbers in sensible ways such as recognizing when an answer is unreasonable; comparing fractions by recognizing their relative distances from 0, 1, or 1/2; shifting easily among fractions, decimals, and percents; and knowing when a mental calculation would be faster than using paper and pencil or even a calculator. In curriculum materials, using numbers in sensible and flexible ways is often referred to as number sense.
Coursework designed for middle grades teachers must help these teachers develop strong number sense in addition to number
skills. The prospective teachers will also need to learn to go beyond procedures to look at the underlying mathematics and try to
make sense of it. One way to accomplish this goal is to provide them with examples of middle grades problems, and if possible,
examples of students' work on these problems, and discuss the strengths and weaknesses of different students' approaches to a
problem. (Books on results of mathematics portions of the National Assessment of Educational Progress and items from the 8th grade
Third International Mathematics and Science Study are sources of such problems.![]() ) For example, suppose seventh
graders have been asked to estimate 316
) For example, suppose seventh
graders have been asked to estimate 316
![]() 16.2. Here are five
possible responses:
16.2. Here are five
possible responses:
| 4500, because 300 | |
| Round 16.2 to 20 and round 316 to 300. My estimate is 6000, minus a little. | |
| You can round 316 to 320 and think of 320 as 32 Then you can write the problem as 25 | |
| 300 | |
| If you multiply 316 and 16.2, you get 5119.2, which rounds to 5100. |
Prospective teachers (who should have already made their own estimates) could then be asked about the mathematical thinking portrayed by each of these solutions. What type of understanding of numbers and operations is represented in each solution? Does proficiency at computational estimation require a different understanding of numbers and operations than is needed to carry out standard computational procedures? Are some procedures and final estimates more, or less, appropriate in different situations, such as when estimating the cost of renting graduation gowns at $16.20 each for 316 students?
Many students in middle grades will not yet have fully developed necessary procedural skills for operations on whole numbers. Middle grades teachers need to understand and be able to explain both the rationale for the steps in whole-number arithmetic algorithms, which build on place value knowledge, and the ways these algorithms are extended to decimal number operations. In particular, the multiplication and division algorithms for whole numbers and decimal numbers need to be understood so that they can be taught in ways that help students remember them without resorting to thoughtless, rote techniques and that serve as a foundation for later learning. Teachers should be able to recognize valid procedures that students sometimes invent to carry out calculations, and to reward those that are based on good number sense. Many times the traditional algorithms can build on students' invented procedures and thus lead students to a better understanding of the standard procedures.
A strong foundation in work with rational numbers is absolutely essential for teaching in the middle grades. Prospective teachers often think that they have this knowledge if they know the algorithms for operations, for example, to invert and multiply when they divide fractions. They are sometimes surprised to learn that there is something to understand about the usual algorithm for dividing fractions and that there are other, equivalent algorithms. Understanding division of fractions requires a deep understanding of what fractions are, and of what division means.
Teachers should understand how decimals extend the place value work from the earlier grades. They should be able to convert easily among fractions, decimals, and percents. They should understand why only repeating decimals can be converted to fractions, and why non-repeating decimals are not rational, thus leading to a discussion of irrational numbers. Their knowledge of positive rational numbers can then be extended to a study of negative rational numbers. Although prospective teachers will have some familiarity with operational properties, the rational number system is usually their first encounter with a field. Teachers should be able to develop, for example, Venn diagrams to represent the hierarchy of the different types of numbers: whole, integer, rational, irrational, and real, and how they are related.
Mental computation and estimation can lead to better number sense. Most middle grades students and some prospective teachers,
when asked to use mental computation, will attempt to mentally undertake the pencil-and-paper algorithm with which they are
familiar rather than use number properties to their advantage (e.g., using the distributive property to find 7![]() 28 or the associative property to think of 7
28 or the associative property to think of 7![]() 28 as 7
28 as 7![]() 7
7![]() 4, or 49
4, or 49
![]() 4). To help prospective teachers develop "rational number sense," tasks can be designed that include
mentally ordering a set of rational numbers (e.g., 0.23, 5/8, 51%, and 1/4) using knowledge of number size; estimating the outcomes of rational number operations
(e.g., 7/8 + 9/10 must be a little less than 2 because each fraction is a little less than 1), and recognizing wrong answers (e.g., 2/3
4). To help prospective teachers develop "rational number sense," tasks can be designed that include
mentally ordering a set of rational numbers (e.g., 0.23, 5/8, 51%, and 1/4) using knowledge of number size; estimating the outcomes of rational number operations
(e.g., 7/8 + 9/10 must be a little less than 2 because each fraction is a little less than 1), and recognizing wrong answers (e.g., 2/3 ![]() 1/2 cannot be less than 1 because there is more than one 1/2 in 2/3). Developing flexibility in working with numbers will take time, even for prospective
teachers, because most have never been asked to think about numbers in these ways.
1/2 cannot be less than 1 because there is more than one 1/2 in 2/3). Developing flexibility in working with numbers will take time, even for prospective
teachers, because most have never been asked to think about numbers in these ways.
Basic number theory has a valuable role to play in contemporary middle grades mathematics and should have a role in courses designed for middle grades teachers. They should experience conjecturing and justifying conjectures about even and odd numbers and about prime and composite numbers. They should have a good grasp of the Prime Factorization Theorem and how it extends to algebra learning. The difficulty of finding the greatest common factor of two numbers can lead students to an appreciation of the efficiency of the Euclidean Algorithm.
Prospective teachers need to attach meaning to very large numbers that they see daily. Developing benchmarks for large numbers (e.g., calculating one's share of the national debt) can lead to a better sense of what these numbers mean. Examples of very small numbers can be found in middle grades science. The difficulty of writing, expressing, and calculating with very large numbers and very small numbers will lead prospective teachers to appreciate the structure and sophistication of scientific notation.
Finally, experiences using ratios as a means of comparison can lead prospective teachers to think about situations that are proportional in nature. For example, when prospective teachers are asked to compare the steepness of two ramps, some do so by comparing the differences between the heights and depths of the ramps rather than by comparing the ratios of these two quantities. A problem such as this one can lead to finding slopes of lines in coordinate systems and understanding what the slope means. Percents are, of course, ratios, and need to be presented as such.
Prospective middle grades teachers should:
| Understand and be able to work with algebra as a symbolic language, as a problem solving tool, as generalized arithmetic, as
generalized quantitative reasoning, as a study of functions, relations, and variation, and as a way of modeling physical
situations. | |
| Develop an understanding of variables and functions, especially of different equivalent relationships between variables. | |
| Understand linearity and how linear functions can illustrate proportional relationships. | |
| Recognize change patterns associated with linear, quadratic, and exponential functions. | |
| Demonstrate algebraic skills and be able to give a rationale for common algebraic procedures. |
Viewing algebra as both a symbolic language useful in mathematics and science and as a powerful tool for making sense of the world is central to prospective teachers' understanding of what algebra is. Only when teachers work with a variety of problems designed to develop this expanded view of algebra will they come to understand what they are required to know in order to teach algebra. Algebra viewed in these different ways subsumes its traditional role of developing the ability to work efficiently and appropriately with symbols.
One way to develop meaning in algebra is to highlight the manner in which algebra is generalized arithmetic, a language that encodes properties of arithmetic operations. A somewhat different way to think of algebra is as an extension of quantitative reasoning in arithmetic situations. If arithmetic word problems are solved by focusing on the quantities in a problem and determining relationships among these quantities before assigning any numerical values to the quantities, it is a reasonable next step to assign variables rather than numbers. Assigning variables to the quantities and setting up equations representing the relationships is then a formalization of reasoning quantitatively about the problem. However, this formalization is not always an easy one. Prospective teachers need practice on solving problems situated in realistic contexts through this type of analysis, which can also help them develop a deeper appreciation of the important role variables play in algebra.
Functions, relations, and variation all play important roles in school algebra. In middle grades these roles are prominent as students come to understand algebraic functions, particularly linear functions and the manner in which they can illustrate proportional relationships. Using qualitative graphs, that is, graphs that have no numbers but that "tell a story," can lead to a deeper understanding of functional relationships. For example, suppose a vase widens rapidly from its base, then has straight sides, then gradually tapers in until the top is congruent with the base. If water is poured into the vase at a steady rate, what will the time/height-of-water graph look like?
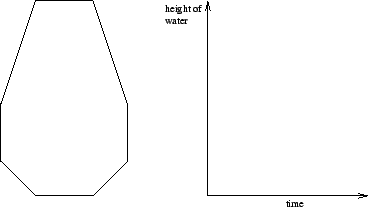
Examples such as this one can provide prospective teachers with a foundation needed to come to better understand how graphs can be used to represent linear, quadratic, and exponential functions, and how tables, equations, and graphs are related.
A study of the mathematics of change can provide a perspective on algebra that will be new to most prospective middle grades teachers. Middle grades teachers should know how to deal with problems involving rate of change, for example, of the growth of a plant, the decline of an endangered species, or of the speed of a car. The accumulation of miles traveled while driving at a certain speed is also a problem of change, and shows the relationship between distance traveled and rate of travel (Noble, Wright, Nemirovsky, & Tierney, 2001). Some elementary textbooks now include problems in which students investigate change. At the middle grades level, teachers who can provide examples of continuous change in situations involving time, velocity, and acceleration and who know how these changes can best be represented can lead students to a better understanding of how quantities such as time and motion are related. Some calculators now have as an accessory a motion detector that can be used to help prospective teachers better understand rate of change.
With technology and the advent of graphing calculators, there is much discussion about what students ought to be able to do with and without calculators. Teachers need to understand the potential that graphing calculators have for the enhancement of student learning of algebra; gaining this understanding requires that they use graphing calculators themselves.
Many curriculum developers say that the study of algebra ought to begin much earlier and extend throughout the grades, that algebra ought to be a curriculum strand rather than a course. For example, the study of patterns and making generalizations based on patterns can begin in the early grades and continue through the middle grades. Preparation of middle grades teachers ought to allow them to teach algebra as a curriculum strand or as a year-long course, depending on a particular school district's plan. To do either successfully, teachers must examine what school algebra is and how it can be taught in meaningful ways at different grade levels.
Prospective middle grades teachers should be able to:
| Identify common two- and three-dimensional shapes and list their basic characteristics and properties. | |
| Make conjectures about geometric shapes and then prove or disprove them. | |
| Demonstrate how rigid motions in the plane result in congruent figures. | |
| Demonstrate understanding of how similar figures result from a dilation, and the role of proportional relationships in
determining similarity. | |
| Demonstrate ability to visualize and solve problems involving two- and three-dimensional objects. | |
| Connect geometry to other mathematical topics, and to nature and art. | |
| Understand the common forms of measurement and choose appropriate tools and units for measuring. | |
| Understand, derive, and use measurement techniques and formulas. |
Prospective teachers have some basic knowledge about shapes and about how to calculate areas and volumes of common shapes, but many will not have explored the properties of these shapes or know why the area and volume formulas are true. The study of properties of shapes should include conjecturing, then proving or disproving to enhance geometric reasoning and lead to an understanding of the role of proof in geometry. The study of three-dimensional shapes beyond rectangular prisms is often new to prospective middle grades teachers, as is visualizing actions of shapes in three-dimensional space. Prospective teachers should develop spatial reasoning ability and should be able to perform such tasks as, for example, envisioning how to slice a cube to get a cross-section that is a square, or a non-square rectangle, or an equilateral triangle, or a trapezoid, or a regular hexagon. Software (e.g., Geometer's Sketchpad, Cabri Geometry, Math Van, GeoShapes, Turtle Math) can facilitate exploration of geometric shapes. Prospective middle grades teachers should have opportunities to become familiar with such software.
Making connections between geometry and other areas within mathematics is an important aspect of preparing teachers to teach mathematics. Reasoning with two- and three-dimensional shapes can lead quite naturally to a study of symmetry and of geometric transformations in general. The coordinate system so often used to represent equations in two variables lends itself well to investigating motions in the plane. The study of rigid motions can lead to an understanding of congruence, and dilations to an understanding of similarity, scale factors, and the role of proportions in establishing similarity. Geometry should also be studied as it occurs outside of mathematics, such as in nature and in art. There are many examples that could be studied, such as in the artwork of various cultures (see, e.g., Washburn and Crowe's Symmetries of Culture or Paulus Gerdes's Geometry From Africa). Geometric transformations can be found in many designs, and recognizing these transformations adds, for prospective teachers, a legitimacy to the study of transformations by middle grades students.
Prospective teachers need to understand what it means to measure---that a quantity is any characteristic (such
as length or rate or number of eggs in a carton) that can be measured or counted using some preselected unit, that the measurement
or count is the value of that quantity in terms of the given unit, and that standardized units are needed for ease of
communication. Formulas for measuring area and volume should be developed in such a way that a teacher could later derive a
formula if it is not remembered. But developing formulas is insufficient; teachers need to come to a deeper understanding of the
quantity being measured. Many prospective teachers relate area only to geometric figures for which a formula can be derived and
often use formulas inappropriately. They do not have strategies, such as decomposing and recomposing figures or superimposing
grids, that lead to ways for finding areas of other shapes. Indeed, the idea that a non-regular closed figure in a plane has an
area needs to be established for some prospective teachers. Part of their confusion stems from a lack of real understanding of
area and of appropriate units to measure area. For example, if given a 3-inch by 5-inch card and asked to use it to measure the
area of a table top, some prospective teachers use the card to measure one table edge in 5-inch lengths, measure the adjacent
table edge in 3-inch lengths, and then are unable to identify a unit associated with the product of the two measurements.
Prospective teachers need experiences that help them better understand the role of units of measurement, choose appropriate tools
and methods for measuring, and recognize the complexity of relationships between different types of measures. Exploring area and
perimeter by holding one measurement constant is such an experience. Other learning situations could involve scale changes in
planes and in space, leading first to problems involving proportional reasoning and measurements of similar figures, and then to
the meaning of congruence of both two- and three-dimensional space. Other forms of common measurement, such as angle measurement,
should be introduced in ways that help prospective teachers make sense of the manner in which these forms of measurement were
devised and are used.
Measurement goes far beyond geometric figures. People have developed a variety of ways of measuring naturally occurring phenomena, from atmospheric pressure to the health of a new-born child, to satisfy the desire to quantify a particular quality. Dava Sobel's book Longitude, the basis of a 2000 PBS program, describes the need for accurately measuring time in order to find a ship's location at sea.
The Pythagorean Theorem and its applications in problems involving lengths of sides of triangles and in the development of the
distance formula can fit well into a study of measurement. There are several proofs of the Pythagorean Theorem that are accessible
to middle grades students. Teachers should have studied such proofs and be able to find, review, and use them in teaching when
appropriate.
The discussion here focuses on general topics included in middle grades geometry and measurement. If they are to teach in schools
where the usual secondary geometry course has been moved to middle grades, teachers will need further preparation, as discussed
earlier.
Coursework should provide prospective teachers avenues to:
| Design simple investigations and collect data (through random sampling or random assignment to treatments) to answer specific
questions. | |
| Understand and use a variety of ways to display data. | |
| Explore and interpret data by observing patterns and departures from patterns in data displays, particularly patterns related
to spread and variability. | |
| Anticipate patterns by studying, through theory and simulation, those produced by simple probability models. | |
| Draw conclusions with measures of uncertainty by applying basic concepts of probability. | |
| Know something about current uses of statistics and probability in many fields. |
Prospective teachers need both technical and conceptual knowledge of the statistics and probability topics now appearing in middle grades curricula. Coursework for prospective teachers should include exploratory analyses of data sets, consideration of the various types of graphs that can be used to portray the data in ways that highlight the important features of the data, investigation of ways of measuring the center and spread of a distribution and how these measures affect decision-making, and the study of relationships portrayed by associations between two data sets (or two variables representing data). To make sense of the statistical information encountered in daily life (such as the accuracy of a political poll that declares a winner of an election or the correctness of a medical experiment that results in new treatment for a disease), a teacher must understand the role of the random selection of samples from a fixed and well-defined population for the purpose of estimating parameters of that population. Prospective teachers should understand the process of making inferences through simulated sampling distributions (which can be done effectively in middle grades) and also see how this process is related to the more mathematically based inference taught at higher levels.
Teachers need to understand that probability, because of its predictive value, can be considered a way of thinking about future events. For example, because the probability of heads is 1/2 (or at least extremely close to 1/2) on any toss of a fair coin, one should not bet heavily that the next toss will give tails, even though the last five tosses were heads. Knowledge that a model providing a theoretical probability can be checked empirically is fundamental to the study of the relative-frequency concept of probability, which is the most useful to the study of statistics at this level. Understanding probability distributions and how they arise leads students to better understand likely and unlikely outcomes. Summary measures for probability distributions are couched in terms of expected values, and expected-value problems should be included in a course for middle grades teachers. Many examples and much class discussion will be needed before prospective teachers can be expected to fully understand the rules for calculating probabilities of compound events made up of independent or dependent events.
Prospective teachers need experiences with designing simple experiments, collecting, displaying, and analyzing data, and using
software that helps them understand how to display and interpret data. Fathom can be used to enhance teachers' learning; DataScope
and ProbSim are available for Macs for use in the middle grades. Tabletop and a student version of Data Desk
have been found useful by some teachers. New statistical software is being designed at University of Massachusetts to be used at
the middle school level.![]()
All of this software can help both teachers and students develop conceptual understanding of statistical and probabilistic ideas. Access to appropriate computer technology is extremely important in helping prospective teachers to develop an understanding of statistical concepts.
Statistics and probability play increasingly important roles in many fields, and attention should be given to some of these roles so that prospective teachers understand the importance of this component of the curriculum.
The content described in this chapter is aimed at providing depth of understanding of the basic areas of middle grades
mathematics. The preparation described here (and more extensively in Chapter 8) should result in teachers who know what it means
to understand mathematics at a level that allows them to teach, and who have confidence in their own ability to engage their
students in a strong core curriculum and prepare them academically for secondary school.
![]()